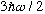Issued Wed, Oct 15 Due Wed, Oct 22

(Required reading for this week: Continue reading Gas. Ch. 6

There are HINTS for this homework.

1) Gas 5-6.

2) Gas 5-7. You only need to do the first part: "Show that is has the form..."

3a) Gas 5-9, but just do it for the two lowest eigenfunctions. Don't forget to normalize! (Please give your wave functions as functions of x, not y.)

3b) Show that your solution for the second eigenfunction in part a) explicitly satisfies the Schrodinger Eqn. In doing so, also explicitly verify that the energy of this state is .

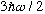4a) A 1 microgram mass sits on a spring, and oscillates with frequency 1 Hz. At the center of its motion, its velocity is 1 micrometer/s. What is the (approximate) value of the energy quantum number "N" which describes this state? (Is this state basically "quantum" or "classical"? Why?)

4b) A CO (carbon monoxide) molecule can be modeled as a vibrating spring. When you have two objects ("C" and "O" here) it might seem to be a different problem than what we've studied so far, but we will show later this semester that, just like in classical physics, you can consider this system to be equivalent to a single object with a reduced mass 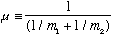vibrating like a simple 1-D harmonic oscillator. CO molecules absorb and emit radiation at a wavelength of 47,000 Angstroms. (In the IR) This corresponds to excitation (or radiation) of this harmonic oscillator system with a change of the quantum number . 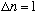Use the above information to deduce the "spring constant", k, between the "C" and "O" atoms in this molecule in MKS units. (Note: M(Carbon)=12 amu, M(Oxygen)=16 amu)

At room temperature, do you think CO molecules will generally be in their vibrational ground state, or some thermal distribution that would include many excited states? (Why?)

5a) part 1 of problem #6-1

5b) Gas. #6-4

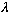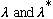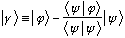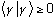Hint for 6-4) Gas' hint is tricky: is complex, so are independent! I have a much simpler hint that should work better for you. Suppose you define the new quantity . It must be true that (because the norm of any vector is always positive definite). Work out the consequences of this fact, and you should be able to show the Schwarz inequality immediately.