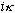 )
and solve for
)
and solve for
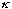 .
It's a quadratic eq, so you'll get 2 solutions. They should be identical to Gas
5.63! (that's what you're trying to show). You'll need to use some trig
identities (e.g expanding cos(2x) and sin(2x)) to do so...
.
It's a quadratic eq, so you'll get 2 solutions. They should be identical to Gas
5.63! (that's what you're trying to show). You'll need to use some trig
identities (e.g expanding cos(2x) and sin(2x)) to do so...
1 Gas tells you to set the denom. of Eq. 5.26 to 0 (first replace
k with
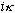 )
and solve for
)
and solve for
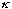 .
It's a quadratic eq, so you'll get 2 solutions. They should be identical to Gas
5.63! (that's what you're trying to show). You'll need to use some trig
identities (e.g expanding cos(2x) and sin(2x)) to do so...
.
It's a quadratic eq, so you'll get 2 solutions. They should be identical to Gas
5.63! (that's what you're trying to show). You'll need to use some trig
identities (e.g expanding cos(2x) and sin(2x)) to do so...
Realize the coolness of what you just did. You took a result from when E>0 (our "R" and "T" result), played a few tricks, and figured out the allowed binding energies for when E<0! When we did these two problems in class, the setup and solutions seemed totally different. Think a bit about the argument for why this works!! Griffith's discussion of the scattering matrix, pp. 66-68, will help. Part of the problem as stated by Gas is to explain what's going on, why this little trick works...
2 Look back at prob. Gas 5.1 (last week) for all the def's. You must set up some convenient incident wave with E>0, and solve for R and T (or all the S matrix elements if you are solving the whole problem at once) You can solve this problem all at once, with incident waves A and D coming in from both sides. Or, you can solve "half the problem" with only a wave coming in from the left. This gives half the S matrix, and you must think of some physical (symmetry) argument to get the other two entries..
3a) Gas (or my notes) has done all the work for you. To normalize, use our old Gaussian integral formula(s)? (Or, just use Gas Eq. 5-146)
b) Take your solution from part a, and plug it in the Schrod. Eqn, i.e.
calculate
 ,
where V(x) is the harmonic osc. potential, and what you should find
after the dust clears is that you get back a constant times the u(x) you
started with. That proves that your u(x) is indeed an eigenvalue. (And, that
constant you get is E...)
,
where V(x) is the harmonic osc. potential, and what you should find
after the dust clears is that you get back a constant times the u(x) you
started with. That proves that your u(x) is indeed an eigenvalue. (And, that
constant you get is E...)
4) I think this one is pretty straightforward, just watch units carefully.
The answer to part b for the spring constant should be in units of N/m (do you see why?) A sloppy American car shock might have a "k" about a few thousand N/m, your answer won't be all that different. Is it a surprise (or a coincidence?) that atomic spring constants might be comparable to macroscopic spring constants? By the way, typical thermal energies in a heat bath are k_B T, where k_B is Boltzman's constant. (Given in the back of Gasiorowicz)
5 The Hermitian adjoint is defined by
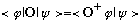 .
.
"O is Hermitian" means
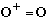 .
.
In general, if
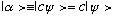 then
then
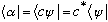 .
.
Remember,
 ,
and the norm of any vector is always real and positive, i.e.
,
and the norm of any vector is always real and positive, i.e.
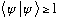
(OOPS. TYPO - that very last relation should be >=0, not 1! (It's real and positive, but doesn't have to be bigger than 1!)