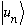 (So,
(So,
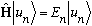 ).
Say there is some other observable B, with associated operator B,
which has normalized eigenfns
).
Say there is some other observable B, with associated operator B,
which has normalized eigenfns
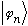 and eigenvalues
and eigenvalues
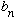 .
.
Issued Wed, Oct 29 Due Wed, Nov 5
Exam II will be Thurs, Nov. 6 at 7:30 PM. It will cover Gas. Ch. 1-6, with most emphasis on new material (since the first exam.)
(Required reading for this week: Ch. 7)
There are HINTS for this homework.
1) You have a particle in a harmonic oscillator with normalized eigenfns
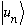 (So,
(So,
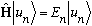 ).
Say there is some other observable B, with associated operator B,
which has normalized eigenfns
).
Say there is some other observable B, with associated operator B,
which has normalized eigenfns
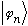 and eigenvalues
and eigenvalues
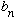 .
.
(So,
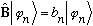 ).
).
Suppose you solved for the eigenfunctions of B, and found the lowest two
are given by
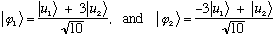 .
.
Now take an electron in the harmonic oscillator, and measure the quantity B.
Suppose you happen to get
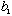 .
Then you go and measure its energy:
.
Then you go and measure its energy:
i) What energies can you possibly measure? With what probabilities?
ii) Say this energy measurement gives you
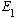 ,
and then you measure quantity B again right away. What is the
probability that you will find
,
and then you measure quantity B again right away. What is the
probability that you will find
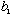 ?
?
ii') Say instead you measure energy, put don't pay any attention to what
you get, then you measure quantity B again right away. What is the total
probability that you will get
 ?
(The answer is different than in ii !)
?
(The answer is different than in ii !)
iii) If you measure B and get
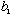 ,
and then measure B again right away, what would you get?
,
and then measure B again right away, what would you get?
But if you measure B, and get
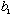 ,
then measure energy, then measure B again (as described in part ii or
ii' above), you don't always get
,
then measure energy, then measure B again (as described in part ii or
ii' above), you don't always get
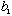 again!
again!
How can this be? Do you think B commutes with H? (Briefly discuss.)
2) Consider a system where
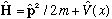 :
:
a) Use Gas 6-64 to show that
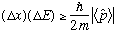 .
.
(This is a kind of screwy mixed up position-energy uncertainty principle)
b) For stationary states (i.e, wave functions that are exact eigenstates of energy) the above uncertainty principle doesn't tell you anything. Why not?
(over ->)
3) A particle is in a harmonic oscillator, with
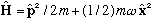 .
.
a) In general, find
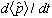 and
and
 .
(Express your answers in terms of m,
.
(Express your answers in terms of m,
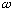 ,
,
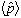 and .
and .
 .)
.)
b) Suppose your particle begins (at t=0) in the ground state,
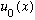 .
.
Is momentum,
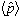 ,
conserved for all time?
,
conserved for all time?
Does the particle's position,
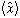 ,
ever change with time?
,
ever change with time?
Does the particle's energy,
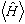 ,
ever change with time?
,
ever change with time?
Hint: Think about using symmetry arguments. I claim you don't need to do any integrals for this part.)
b') Repeat part b, if you start (at t=0) in the first excited state,
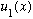 .
.
Extra Credit: 3c) Repeat part b if you start in a mixture of the
first two states:
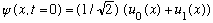
(The next problem is not extra credit, only 3c above was...)
4) Gas 6-12a only.
Note, Gas. asks you to solve the equations you get for x and p simultaneously. That means explicitly find <x>(t) and <p>(t)!
You should assume your particle starts localized at some given
<x>(0), with some given <p>(0), at time 0, and write your
answer in terms of those 2 givens (and the other constants in the Hamiltonian,
m,
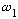 ,
and
,
and
 ,
of course)
,
of course)
| 3220 main page | Prof. Pollock's page. | Physics Dep't | Send comments |