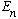1) This problem is about collapsing wave functions. Remember, if you measure some operator, like H, and get a result 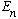, then you have just collapsed the wavefunction into the corresponding eigenfunction .

ii) I gave you 2 equations (for phi1 and phi2 in terms of u1 and u2.) They are linear, so it's quick and easy to invert them, i.e. solve for u1 and u2 in terms of phi1 and phi2. This is very useful here! (If you have u1 in terms of phi1 and phi2, you can answer this problem instantly.)

ii') To find the total probability of measuring b1, you must consider all the different ways it could happen. (First assume that the energy measurement gave some specific result, and find the probability of then getting b1. Then assume that the energy measurement gave another possible specific result, and so on. Now, how do you combine these to find the total probability of getting b1, without knowing or caring what value you got for energy when you measured it? That is what the question is asking.The answer can be expressed exactly, no calculator needed, really, and I get a rather high total probability, bigger than 80%.

2a) All you have to do is figure out one commutor, that's it.

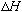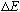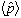b) What is (i.e. ) for a stationary state? What is ? The answer to both questions is simple as can be, in form! (There are various tricks to see the latter, e.g. look at Gas 6-72, and think about the time dependence of <x> in a stationary state, i.e. a state with a pure energy...)

3a) You don't have to reinvent the wheel here. Make use of equations we derived in class, like Gas. Eqs 6-68, 72 and 76. This is meant to be quick.

b) and b') You know the time dependence of energy eigenfunctions (it's easy!) and you know the definition of expectation values. (You should not have to do any integrals, think about symmetry!)

Your final answer, if you think about it physically, should be a little weird and bothersome! (Shouldn't harmonic oscillators oscillate?) If you want to get a better feel for what's going on, try the Extra Credit

4) Same comments as 3a - make use of Gas. 6-68, 72 and 76. (Combine the eqns for d<x>/dt and d<p>/dt, by differentiating the d<x>/dt equation with respect to time again, to get a simple second order diff.eq. you can solve immediately for <x>(t). Once you know <x>(t), Gas. 6-72 tells you <p>(t) with minimal work! The differential equation does require remembering a basic little trick about 2nd order ODE's, it's in Boas, Ch 8.6(?) if you've forgotten.