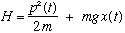Issued Wed, Nov 5 Due Wed, Nov 12

Reminder: Exam 2 will be Thur, Nov 6 ,7:30 PM

Required reading for this week: Ch. 9 (only pp. 160-161), and Ch. 10.

Note: The object in the first problem is to start thinking in an "operatory" way, rather than a "wavefunctiony" way. E.g. you should not do (or even write down) any explicit integrals. Think about operator properties!

There are HINTS for this homework.

1a) Gas. 7.3 (Give an explicit formula for the result)

b) Gas. 7.8 (See hints!)

2) Gas 7.11a only.

Don't just use the results from H directly, but rather SHOW that N has eigenvalues n=0,1,2... from scratch, using the same ideas and principles as Gas did (and we did in class) for showing that H had discrete eigenvalues.

3) Consider the Hamiltonian describing a one-dimensional particle in a gravitational field, .

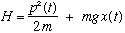a) Calculate the equation of motion for the operators x(t) and p(t),

using (7-63), and the commutation relation .

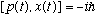b) Show that the equation of motion is just the classical equation of motion.

c) Solve for p(t) and x(t) in terms of p(0) and x(0).

(The only other constants appearing in your answer should be m and g).

d) Show that . (Which tells you that operators that commute at the same time need not commute at different times.)

4) Use separation of variables in Cartesian coordinates to solve for a single particle in an infinite cubical well ("particle in a 3-D box"):

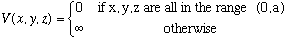
a) Starting from scratch, find the stationary state wave functions, and corresponding energies. (I sketched this out in lecture: fill in any missing details that you feel you need to understand where Gas. Eq's 9-7 and 9-8 come from.)

b) Find the lowest 6 energies. (Call them E1, E2, ... E6) and find the degeneracy of each of these energies.

c) What is the degeneracy of E14? Why is this case interesting?

5) (over ->)

5) I thought we'd do something a little unusual here. There are a number of equations in Gas. Ch. 10 which he writes down and says "it is easy to show" or "it follows that", "and so on", etc. (the usual physics textbookese!) Problem #5 this week is to show the steps Gas. left out to get the statements below.

Note: These problems are essentially pure math. You should be able to get them even if we haven't reached the eq'n in question yet in lecture. In fact, it should help the lectures make more sense if you've already proven these eq'ns ahead of time.

The unnumbered equation one line past 10-12

Eq'n 10-25

The statement " =0", two lines above the paragraph above Eq'n 10-27

That 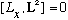(i.e. part of the "and so on" following 10-27.)

(There are plenty more of these if you like them! Let me know...)