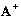1a) Matrix elements of the operators A and 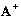between energy eigenstates are easy, especially given that we proved in class

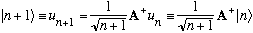. (I'd use Gas' hint backwards, to figure out what A does. Given this, you do not need the results of Gas. problem 1, in fact you'll end up deriving that.)

Once you know matrix elements of A and A(dagger), you can (fairly easily) find a linear combination that tells you matrix elements of x.

1b) A little thought (problem 1a helps!) should tell you what <n|x|n> is, without any real work at all. As for <n|x^2|n>, there are many ways to find it without doing any integrals. You could work out x^2 in terms of A and A(dagger) (and their squares). That's "straightforward but tedious". Or, you could be trickier. E.g., if you use the result of problem 5-18 (you may do so as long as you can convince yourself you understand where it comes from!) then you'd have a quick and easy way to find <x^2> here. Or there's a totally different way that doesn't require you to take anything "on faith", and takes advantage of your work in problem 1a. It makes use of "completeness", Gas. Eq 6-45, . You can sandwich this "1" inbetween the two x's in x^2. (Note: the summation index you use is a dummy - choose one that's DIFFERENT from the index of the state in the bra/ket!) You will then have an infinite sum, but for any given term you only need to know a matrix element of x, most of which (from #1a) vanish. So, the infinite sum really has just two terms.

2) In class we went through the derivation of the energies of the harmonic oscillator (i.e, of the eigenvalues of H) just thinking about commutators and ladder operators. In this problem, you should do pretty much exactly the same. The operator is now N, rather than H, but they are extremely similar. The object is for you to go through the derivation of eigenvalues, following the logic of how ladder operators affect the eigenvalues (why must there be a lowest state for N? Can you quickly show that N can't have a negative expectation value?), etc...

3) This should be a straightforward application of 6-63. (It's not a harmonic oscillator problem, so don't use anything to do with A's)

(I didn't ask you to prove it, but do you see why our usual relation, [p,x]=-i hbar, immediately proves that [p(t),x(t)]=-i hbar?)

4) Part a is for your own practice. Do as little or as much work as you like. The answer is Gas 9.7 and 9.8. I just want you to make sure you have a sense for where it comes from.