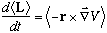Issued Wed, Nov 12 Due Wed, Nov 19

Required reading for this week: Finish Ch. 10, start Ch. 11

There are HINTS for this homework.

1) Recall that Gas. Eq's 10-21 through 10-23 were derived assuming the special case V=V(r), i.e. a purely central potential. Drop this assumption, and prove that, in general, .

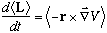Show that in the special case V=V(r), this reduces to conservation of <L>.

(N.B., this problem is the quantum version of the classical equation 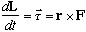, i.e. torque gives the rate of change of angular momentum)

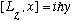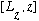2a) Show that . Find and .

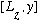b) Using Gas. Eq. 10-62, expand to find approximate (polynomial) formulas valid for x<<1. (Expand to "next to leading order", i.e. giving the leading two nonzero terms in each case.) Verify that the j's are finite as x -> 0, but the n's are not.

Also, expand 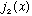to "leading order", i.e. giving the leading power of x only, and verify that Gas 10-66 gives the correct answer for l=0,1, and 2.

c) (We talked about the spherical harmonics in class already. Gas. has them written down on pp. 196-7.) Reexpress the spherical harmonic with l=0 (i.e. ), and all three spherical harmonics with l=1, (i.e. 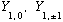) purely in terms of x, y, and z rather than 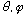. (See Fig. 10-1 on p. 174 for Gas' conventions on radial coordinates) (Gas. Eq. 11-60 tells you his sign convention to get spherical harmonics with negative m's)

3a) A semiconductor device called a "quantum dot" is essentially an electron trapped in a spherical well. Suppose the well radius is 10 A. (model the walls as perfectly reflecting, i.e. it's an infinite well.)

Find the emission frequency (in Hz) of radiation from this electron due to transitions from the 1st excited state to the ground state. What part of the EM spectrum is this? Note: No serious calculations required! Gas. (p. 180) has everything you need to deduce the answer with minimal work.

3b) Given a particle like in part a, in a well of arbitrary radius "a", with l=1: find a simple , analytic, approximate expression for 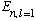if n>>1.

4) Gas #10-6 (Ignore his question "what is it for ka large?" - I claim the answer doesn't really care whether ka is large, small, or whatever!)