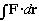 ,
or
,
or
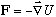 ,
so what one is doing is fundamentally the same as Newton's F=ma :
,
so what one is doing is fundamentally the same as Newton's F=ma :Physics 3220, Fall '97. Steve Pollock.
Back to the list of lectures
Prerequisites are 2140, 2170 and 3220, plus differential equations and linear algebra. Talk to me if you have any possible deficiencies.
We will use cgs units, mostly, plus eV and Angstroms. (More on this soon!)
What is Quantum Mechanics?
Q.M. is a new (and absolutely necessary) way of predicting the behavior of microscopic objects. It is based on several radical, and generally also counter-intuitive, ideas:
1) Many aspects of the world are essentially discontinuous
2) Many aspects of the world are essentially probabilistic, not deterministic.
Bohr: "Those who are not shocked when they first come across quantum theory cannot possibly have understood it."
In order to get some perspective, let's step back, and ask
What is classical mechanics (C.M.)?
It is, most simply put, the study of how things move! Given a force, what is the motion? So, C.M. studies ballistics, pendula, simple harmonic motion, electrons in E and B fields, etc. Then, one uses the concept of energy (and conservation laws) to make life easier. This leads to new tools: the Lagrangian (L) and Hamiltonian (H). H(x,p)=T+U (or L(x,v)=T-U) describe systems in terms of the energy (kinetic and potential). With these, C.M. becomes more economical, and solving problems is often simpler. (At the possible cost of being more formal, and maybe less physical?)
Of course, U = Potential =
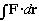 ,
or
,
or
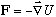 ,
so what one is doing is fundamentally the same as Newton's F=ma :
,
so what one is doing is fundamentally the same as Newton's F=ma :
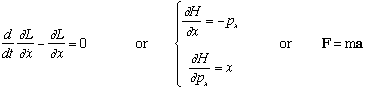
The general goal is to find the equation of motion of pointlike objects: x(t) and p(t), position and momentum as a function of time.
Then, you can add complications:
E.g. rotation (moment of inertia, L=rxp, more complicated bodies)
also normal modes, e.g. coupled pendula:
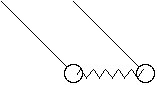
This kind of problem really shows the power of the Hamiltonian formalism. The
motion looks very complicated, but turns out to be a simple superpositions of 2
basic motions:
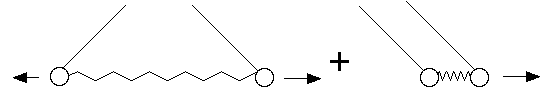
Q.M. is about the same basic thing: Given a potential, what is the motion? It's just that Q.M. tends to focus on small systems.
(Technically, systems with a small action
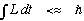 )
)
Having just completed C.M., your initial reaction may be "but, size doesn't matter"! After all, neither L nor H cares about size, and C.M. often deals with so called "point objects". (Isn't a point plenty small? )
Unfortunately, it turns out that in a certain sense, everything you learned in 3210 is WRONG!
To be a little more fair, the techniques of 3210 are fine, but only if applied to real-world sized objects. Size doesn't matter up to a point, but somewhere C.M. finally breaks down. If you try to apply the 3210 L (or H) formalism to an electron in an atom, or an atom in a trap, or a quark in a proton, or a photon in a laser beam, or many other such problems, you will fail big time!
It's not just that the equations are wrong. You can't patch them up with some clever correction terms, or slight modifications of the equations, like relativity does at high speeds. The whole MIND SET is wrong! You cannot ask for (x,p) as a function of time. It's not well defined! Point particles do not exist. Particles have a wave nature, and waves have a particle nature. There is a duality in the physical world which is simply not classical.
So, we must start from scratch, and develop a whole new framework to describe small systems. There are many new ideas involved. Some are formal and mathematical, some are rather unintuitive. I will try to motivate as much as possible, and we'll study plenty of examples. Quantum mechanics comes from experiment! Feynman says that the one essential aspect to learn Q.M. is to learn to calculate, and we will basically follow this idea.
Q.M. is great fun: very weird, sometimes mysterious. Philosophers still argue about what it all means, but we will take a "physicists view", mostly. Issues of interpretation can come later. As a colleague of mine once explained, it's kind of like trying to learn Swahili slang. First, you must learn a new language, and then you must learn a new culture, and only then can you finally begin to truly understand the slang...
Our first topic, which begins in Gasiorowicz Ch. 1, is "The Limits of Classical Physics". We will learn about a number of key issues which arose around the turn of the 20th century. At that time, physics was in something of a state of unprecedented turmoil. On the one hand, there were countless spectacular success stories. Don't think that the physics of 1890 was primitive or pathetic. Working knowledge among physicists of thermodynamics, E+M, optics, classical mechanics, fluid dynamics, and much more, was far more sophisticated than many of us have today(!) Some physicists even thought they might be very close to understanding everything...
On the other hand, there were more than a few confusions (radioactivity was mysterious, discrete lines in atomic spectra were not understood, and much more) and there were several very dramatic failures. That is, there were clear and essentially unambiguous predictions of classical physics that were experimentally shown to be plain dead wrong. It is useful to look at a few of these failures in some detail, to see how QM arose historically, solving the puzzles and failures one by one, developing over a period of about 20 years into a well defined branch of physics.
(N.B.: the majority of textbooks treat QM in this way, motivating it historically. Griffiths, interestingly, does not bother with this. He just presents the ideas of QM straight away, and begins deriving and discussing the consequences immediately. Griffiths' book is very fresh, and will be a useful supplement to Gasiorowicz, but his approach means it won't be until Ch. 2 that we can start to connect to Griffiths...)
There are two historic tracks leading to QM:
1) The values of energy exchange are discrete (Planck, Einstein, Bohr)
2) There is a wave-particle duality. (Photoelectric/Einstein -> De Broglie -> Schrodinger -> Born -> Dirac pulled it together)
One of the first big failures of C.M. was Blackbody Radiation. A
complete study of this topic requires just a little more thermo than you
probably have, but let's look at some of the basic ideas. If you heat any
object, it will emit radiation. The same phenomenon occurs if you sit inside of
a cavity, with walls made of any material. If the walls are warm, there will be
an energy density of radiation in the cavity. (The emission of energy from an
object, and the energy density inside a cavity, are simply related by geometry)
The total power emitted, you may recall, is given empirically by the
Stefan-Boltzmann law,
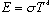 .
We can also ask: "how much energy is there in a cavity at some given
frequency as a function of temperature T?"
.
We can also ask: "how much energy is there in a cavity at some given
frequency as a function of temperature T?"
u
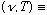 Energy/Volume/(unit
Frequency), or in other words
Energy/Volume/(unit
Frequency), or in other words
u
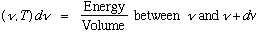
Kirchoff and Wien (1894) used general thermodynamics arguments to argue
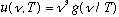
(g is some unknown function, but this formula tells how u depends on frequency
and temperature). Wien had a model, which gave
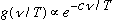
(this turns out to work o.k. for large frequencies, but not for small ones)
His model was funky, and not very general.
Rayleigh (1900) made a more general argument, using the known laws of classical thermodynamics and statistics, and derived
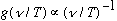 .
.
We'll sketch his derivation below - it was classical and rigorous. The depressing thing was, it was also wrong. The bottom line is that Rayleigh got
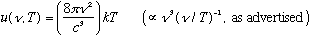
where k is a constant (Boltzmann's constant) and c is the speed of light.
Here's a sketch of this formula, and the experimental data, for u as a function of frequency: (it's now called Rayleigh-Jeans, because Jeans found a small error in Rayleigh's original derivation)
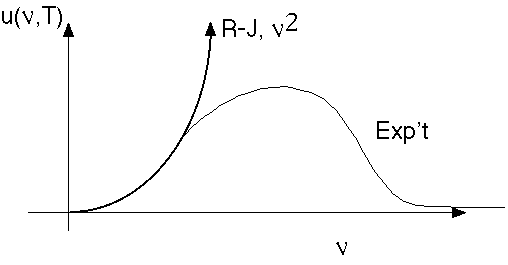
Note that the area under the experimental curve is finite, but under the R-J curve is infinite. The R-J formula is blowing up at large frequencies (the so-called UV region), and this disaster was called the Ultraviolet Catastrophe. When integrated over frequency blows up, which means that a cavity at finite temperature has an infinite total energy inside! The only conclusion to draw is that one or both of our assumptions is false. But, they seem so general!
Max Planck, also in 1900, was interested in this problem. The first thing he did, which physicists today still love to do, was to find a mathematical FIT to the data. This was not a derivation, there was no real physics involved yet, but in a remarkable show of ingenuity he discovered that the formula
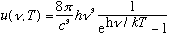
fit the data very well. (This formula had one adjustable parameter, h, now called "Planck's constant", which you could twiddle to change the curve and make it match the data. h=6.6*10^-27 erg s in cgs units, and it is a universal constant. No matter what material a cavity is made of, this same constant always fits the energy spectrum). Note that:
* this formula is indeed of the form
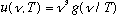 ,
which is good.
,
which is good.
* at large frequencies
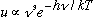 ,
which matches Wien's model result.
,
which matches Wien's model result.
* at small frequencies
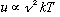 ,
which matches the Rayleigh-Jeans result.
,
which matches the Rayleigh-Jeans result.
(Use Exp(x) = 1+x, for small x, to show this)
* It's pretty inobvious, but the fit to data is glorious. (See e.g. COBE data for the temperature of the universe as a whole, or other COBE related info. )
* It solves the UV catastrophe by getting a maximum into the curve.
* You can integrate this formula, and you find
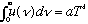 (i.e. Stefan-Boltzmann is recovered)
(i.e. Stefan-Boltzmann is recovered)
But why is this the right form? What was wrong with R-J's derivation? Planck started thinking hard about how to derive this formula, work which he later called the hardest of his life.
| list of lectures | 3220 main page | Prof. Pollock's page. | Send comments |