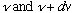 is
is Physics 3220, Fall '97. Steve Pollock.
Here is the Next lecture
Back to the list of lectures
(1) (Geometry, and E+M) The number of different standing EM
waves (i.e. the number of distinct modes) that fit in a box, with
frequency between
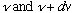 is
is
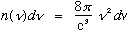 .
.
(Big frequency <=> small wavelength <=> more ways to fit in a given cavity)
Reason: In a box of size L, a mode is characterized by integers n, such that:
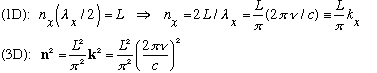
The total # of modes is the total # of distinct integer triples n
satisfying the above eqn (with frequency between
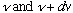 ),
or in other words the volume of a shell in "n" space (in the 1st
quadrant, since the n's are all +'ve):
),
or in other words the volume of a shell in "n" space (in the 1st
quadrant, since the n's are all +'ve):
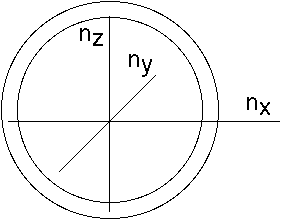
# modes = shell volume/8
=
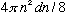
Using the formula above for n, this is
=
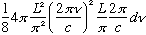
=
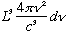
(Note the L^3 = Volume out front)
N.B.: you still need to multiply this by two, because light has 2 polarization states for any given frequency, each of which gives an independent "mode".
(2) Equipartition: The average energy associated with each independent wave pattern (or mode, described above) is kT, where k is Boltzmann's constant, and T is the temperature in Kelvins. (You can think of each wave as like a harmonic oscillator with 2 degrees of freedom, E and B, or KE and PE, each of which should get kT/2. These degrees are distinct from the polarization) If you like, you can think of a thermodynamic derivation of average energy. If energies are Boltzmann distributed, then
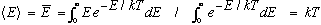
Putting (1) and (2) together gives
u
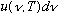 = (# modes in
= (# modes in
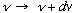 /volume)(Average
energy/mode), i.e.
/volume)(Average
energy/mode), i.e.
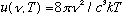 (As claimed above)
(As claimed above)
As we saw before, this formula is a catastrophe in the UV (high frequencies, or short wavelengths). It totally fails to describe the data, and when integrated over frequency blows up, which means that a cavity at finite temperature has an infinite total energy inside! The only conclusion to draw is that one or both of our assumptions is false. But, they seem so general!
But why is this the right form? What was wrong with R-J's derivation?
Assumption 1 is nothing more than geometry, so it didn't seem like this is
where the flaw should lie. In any case you expect that
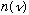 would have to grow with frequency. So modifying this equation will never make
would have to grow with frequency. So modifying this equation will never make
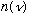 "turn over", which is what Planck needed. Also, at this time it was known that
the derivation of the specific heat of solids was not working. This argument,
too, was based on equipartition. So, it seems like assumption 2 is what's
wrong...
"turn over", which is what Planck needed. Also, at this time it was known that
the derivation of the specific heat of solids was not working. This argument,
too, was based on equipartition. So, it seems like assumption 2 is what's
wrong...
Planck asked the following question: WHAT IF each vibrational mode does
not have a continuous distribution of energies? What if only certain
discrete energies (integer multiples of
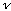 )
are allowed? This is certainly a crazy idea - classically, given a frequency,
the energy is determined by the amplitude of oscillation, and any
energy is o.k. But Planck followed this through...If only these certain
energies are allowed, i.e. E=nh
)
are allowed? This is certainly a crazy idea - classically, given a frequency,
the energy is determined by the amplitude of oscillation, and any
energy is o.k. But Planck followed this through...If only these certain
energies are allowed, i.e. E=nh
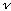 (with n an integer):
(with n an integer):
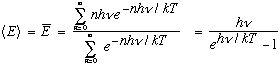
This is just what was needed! Plug this in instead of the old result, and out comes Planck's formula. The exponential takes over at large frequencies, making the energy density turn over. By the way, to get the last result, use two identities (that are easy enough to verify. The first is a Taylor expansion, the second is d/dx of the first, slightly massaged!):
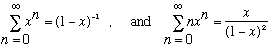
Planck thought this "quantization" or discretization of energy had something to do with the interface between light and matter. That is, he thought that matter (the cavity walls) could only dump energy into the radiation field in lumps or blobs, with E=h nu. But Einstein saw this derivation, and took the idea further. (much to the chagrin of Planck!) Einstein asked whether it might not be a fundamental property of radiation itself that it can only have certain discrete energies (which depend on frequency) This idea had many consequences, some of which we shall investigate.
Let's look at the sorts of scales involved (h is a very small number)
First, a list of some very handy numbers:
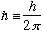 =1.05
=1.05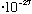 erg s = 6.6
erg s = 6.6
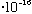 eV s (Planck's constant, "hbar")
eV s (Planck's constant, "hbar")
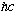 =2000
eV
=2000
eV
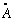
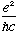 =1/137.
("The fine structure constant", e is the charge of the electron)
=1/137.
("The fine structure constant", e is the charge of the electron)
(We will use the system of units where electric force is simply F=e^2/r^2, no 4
pi's or epsilon_0s. Thus, e^2 has units of dyne cm^2 = erg cm, and
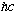 has exactly the same units!)
has exactly the same units!)
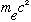 =511*10^3
eV (electron mass) (N.B. Gas.' Appendix, p. 460, gets the electron mass wrong
- it's 9.1
=511*10^3
eV (electron mass) (N.B. Gas.' Appendix, p. 460, gets the electron mass wrong
- it's 9.1
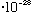 g,
NOT
g,
NOT
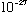 !)
!)
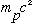 =938*10^6
eV = 2000
=938*10^6
eV = 2000
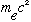 (proton mass)
(proton mass)
Next, some common simple relations:
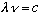 (wavelength*frequency = c, always true for light)
(wavelength*frequency = c, always true for light)
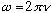 (converts frequency to "angular frequency")
(converts frequency to "angular frequency")
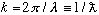 (k is "wavenumber", lambdabar is "reduced wavelength")
(k is "wavenumber", lambdabar is "reduced wavelength")
E = mc^2
An example, with some typical numbers:
How many photons does a typical light bulb emit per second?
If light has frequency
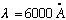 (visible) = (6000)
(visible) = (6000)
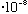 cm = 6
cm = 6
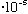 cm,
cm,
then its minimum allowed energy (the energy of a single "photon") is
E= h nu = (6.6
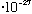 erg s) *(3
erg s) *(3
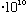 cm/s)/(6
cm/s)/(6
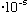 cm) = 3.3
cm) = 3.3
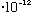 erg
erg
N.B. Another way to do the same:
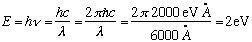
Now, a 100 Watt bulb = 100J/s = 100*10^7 erg/s.
Since each photon has an energy (above) of about 3.3
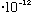 erg, this bulb emits about 10^9/(3.3
erg, this bulb emits about 10^9/(3.3
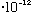 )
= 3
)
= 3
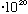 photons/sec.
photons/sec.
No wonder you never noticed that they're discrete!
Is there any other evidence that photons are quantized? (I.e., that energy in light always comes in bundles of E=h nu?) Another historical indication came from the photoelectric effect:
If you irradiate metals with light (EM radiation), electrons may come out. (You can do e/m measurements, with E and B fields to verify that they are indeed electrons!) . It is observed experimentally that there is a minimum threshold in frequency (color) of the light required to get any electrons out at all. If the frequency is lower than this threshold, no electrons come out. If the frequency is above the threshold, then the number of electrons emitted per sec is proportional to the intensity (brightness) of the light. But the energy of the emitted electrons is independent of the intensity of light; instead, the energy of electrons is proportional to the frequency of the light. Furthermore, light (above threshold) begins emitting electrons immediately.
Classically, this is not right! There is an unambiguous prediction, from classical E+M, that says the energy of the outgoing electrons should be proportional to the intensity of the incoming light. . Also, the amount of time required to release the first electrons should increase as the light intensity goes down. However, this is not what is observed in the lab.
Einstein, following up on Planck's idea, argued that the incoming light brings in bundles of energy, E= h nu. So, conservation of energy argues:
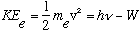 .
.
The electron gains a kinetic energy, KE, by absorbing a photon with energy
h nu. (W is the "Work function" of the metal, which is just the binding energy, or potential energy, of the initial electron)
Since electrons are initially bound by W, the photon has to bring in at least that much energy to allow the electron to escape. That's why there is a threshold frequency. This simple formula explains all the photoelectric observations - the linear connection between energy and frequency, and the independence of energy on light intensity. Not only that, it predicts that the proportionality constant between light frequency and electron energy is the same constant as found in Planck's blackbody curves. These experiments are as different as can be, but "h" came out the same, no matter what metal was used (different W's, which is material dependent, but universal "h")
Milliken (1916) verified this quantitative prediction of Einstein (even though he thought it was nonsense, a throwback to the old discredited idea of "corpuscular light" invented by Newton, and disproven by double slit experiments, diffraction and refraction, in the 1800's!)
If light comes in bundles, are they really little particles of light? (Photons?) Planck thought that this quantization of energy wasn't intrinsic to light, but had to do with light/matter interactions. The photoelectric effect doesn't fully resolve this question, but the Compton Effect basically does.
Compton (1922) argued that if light exists as particle-like photons, these photons should behave like particles. He made some simple arguments for what the scattering of a photon from an electron should look like, assuming it's just a (relativistic) billiard ball problem. To see this, we need to quickly review a couple of basic relativity equations. In particular, we need to know: If E = h nu for photons, what is the momentum of such a photon?
Einstein's relativity formulas says that for a free particle with rest mass m0, the total energy, E, is related to momentum and mass by
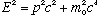
There is also sometimes a "relativistic mass", m, defined such that E = mc^2,
and p=mv (the same old equation for nonrelativistic momentum, but using the full m, not the rest "mo")
If you plug E=mc^2 into the left side of the boxed equation, and p=mv on the right side, and solve for m, you find
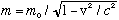
As a little check, consider what you get when v<<c (nonrelativistic limit)
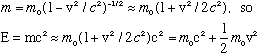
So the total energy is the "rest energy" (just some fixed constant value, which we usually don't pay any attention to) plus the classical nonrelativistic "kinetic energy", 1/2 mv^2, as it should be.
Also, notice that if m0 is finite, v could never equal c, because then m and E would blow up! But, if m0=0, then you're o.k. - photons travel at c, and they have zero rest mass. In this case, the boxed equation on the previous page says
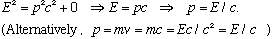
This gives the relativistic connection between E and p for photons.
Now, consider the scattering of light off of electrons, something which can easily by measured experimentally. Classical E+M can calculate this process! What you find is that light of some given frequency sets the electrons oscillating with that same frequency, which in turn re-radiate at the same frequency. The reradiated light will be emitted in all directions, so, light coming in from some direction scatters into other directions, but without any change of frequency.
Compton, however, decided to take seriously Einstein's idea that light scattering off electrons is more like a billiard ball collision (i.e. treat light as pointlike, rather than wavelike), and got a rather different result:
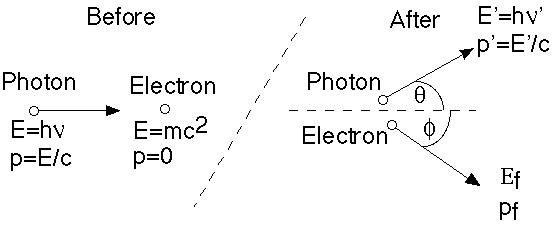
Compton calculated the outgoing frequency, nu', as a function of angle (Classically, nu' = nu)
The algebra is a wee bit ugly, but just use conservation of energy and p:
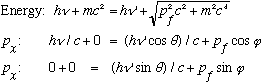
Take the last 2 lines, get the pf terms by themselves on the rhs, square, add:
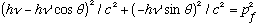
Take the 1st line, get the square root by itself, square, and plug in this last result:
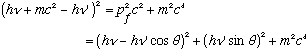
Expand both sides, noting cos^2+sin^2=1:
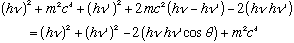
Cancel common terms on both sides:
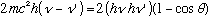
(Note the typo in Gas, between 1-24 and 1-25). Now use
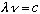 ,
cancel 2c^2:
,
cancel 2c^2:
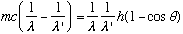
or, finally,
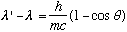
| list of lectures | 3220 main page | Prof. Pollock's page. | Send comments |