Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 1, lecture 3 (Wed 8/29/97)

Here is the Next lecture

Back to the list of lectures

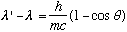
The combination out front, h/mc is called the "Compton wavelength of the electron", and has numerical value 2.4*10^-10 cm. This result is a radical departure from classical E+M. Compton observed this shifted wavelength in the lab. The shift is very small, only becoming noticable when wavelength is itself of order around 10^-10 cm, i.e. high energy x-rays. Compton also saw some photons scattering with unshifted wavelength. This arises when the object being bounced off is not an electron, but an atom, with such a large m that the frequency shift is negligible! Although historically there was some dispute (led by Duane, of CU physics "fame", then in the East coast), this result stands out as a clear confirmation of the particlelike nature of waves.

Given this clear result, De Broglie in 1923 suggested that perhaps particles

might also have wavelike nature too! For photons, we've already seen

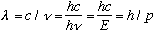. So, what if we were to postulate that

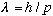is true in general? I.e., what if particles have a wavelength too?

(Note: De Broglie made the argument a little differently - he first asked what to expect if the photon had a small nonzero mass, and finally generalized to arbitrary mass, but still came up with the above formula) The first experimental verification of this, by Davisson and Germer, involved the scattering of low energy particles (electrons) off a crystal surface. They saw a diffraction pattern in the scattered particles, implying that the particles had behaved as waves!

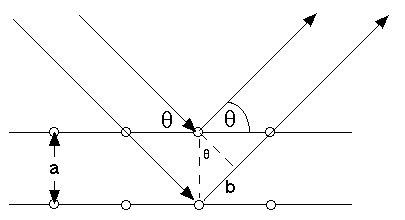
From the picture, we see b/a=sin(theta)

So, the extra distance traveled by the lower electron "ray" is 2 a sin(theta)

If this is an integer number of electron wavelengths, we expect constructive interference

If electrons were truly just particles, they should scatter every which way off a crystal. Particles can't constructively/destructively interfere. But sure enough, at those special angles theta where 2 a sin(theta)=n lambda, one sees a large flux of electrons, and at other angles there are nearly none. The quantitative connection between momentum (or energy, via Einstein's equations) and wavelength were quantitatively verified in these experiments, and many more since then involving neutron scattering, alpha particles, He atoms, and much more....

Here's a numerical example to see the sorts of scales involved. If the crystal surface is Nickel, "a" is 2.15 Angstroms (this is known from x-ray crystallography, e.g.) To see any evidence of diffraction, you need wavelengths roughly this size...

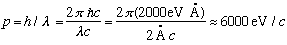
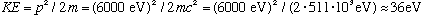
(That's a pretty low energy to control electrons. The experiment was tough) Note that if you want neutrons to have the same wavelength, they must also have this same p, but that means with their larger mass that their kinetic energy will be 2000 times smaller, or about 0.018 eV!

If particles have wavelengths, how come you haven't noticed me diffracting through the classroom doorway when I come in? A typical momentum for me might be p=mv = (50*10^3 g)*(100 cm/s), so my wavelength is

h/p = (6.6 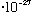erg s)/(5*10^6 g cm/s) = 1.3*10^-33 cm.

Protons have a "size" of about 10^-13 cm, this wavelength is SO tiny you'll never notice it!

At roughly this same time in history, Rutherford (and his students, Geiger and Marsden, 1911) aimed alpha particles at metal foils. They learned that the atom is mostly empty, and they constructed a model in which the proton was a heavy pointlike object in the center, and the electron was in orbit, like a little planet. The idea was appealing, and had some nice features, but it also had some serious flaws:

1) Electrons in circular orbits must, by classical E+M, radiate. The calculation of collapse time can be done in E+M II, and is about 10^-10 sec. We'd all disappear in a puff of radiation in a nanosecond!

2) This picture has no explanation for Balmer's formula which reproduces the experimental spectrum of hydrogen, namely

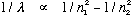
(n1 and n2 are integers)

Bohr (1913) made the first attempt at a "quantum explanation" for the structure of atoms, hydrogen in particular. This was not yet a real QM calculation, but it did have some correct elements, and it helped point Schrodinger, Heisenberg, and others in the right direction not so much later.

Bohr's postulates were as follows:

(1) Electron orbits have |L|=rxp= 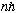("Quantized angular momentum")

(2) Electron orbits are stationary states, so they do not radiate energy.

(3) Electrons can jump from one allowed orbit to another, releasing (or absorbing) a single radiation quantum (a photon), with energy given by

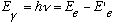
For the rest, classical physics was supposed to hold.

These postulates were very ad hoc, did not have any clear underlying fundamental physics behind them, but still they did a decent job of describing the rather mysterious experimental facts. (We shall see, by the end of this semester, what the real underlying physics is, and we will derive a far more sophisticated picture of the hydrogen atom which has some of the features Bohr was guessing at...) In any case, let's now examine the consequences of Bohr's postulates:

For an electron (charge -e) in a circular orbit. (radius r) about a massive central proton or nucleus (charge +Ze), classical Newtonian physics says the

electric attractive force = Ze^2/r^2 = mv^2/r (= ma, uniform circular motion)

Bohr's first postulate says |L| = mvr = n hbar. Use this to get rid of "v" above:

Ze^2/r^2 = (mv)^2/(mr) = (n hbar/r)^2/(mr), or, solving for r,

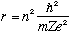
This tells us that the "allowed" orbital radii are quantized.

Next, again using mvr = n hbar, now solving for v with the above r, gives

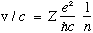
Also, the total energy of the electron, kinetic + potential, is

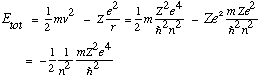
The negative sign means the electron is bound. The integer n in the formula means the energies are quantized, only certain energies are allowed. From the third postulate, emitted light will have frequency

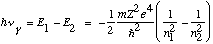
This is Balmer's formula! The numerical coefficient out front is even correct.

Some numbers and scales:

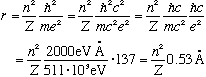
This number, 0.53 A, is called the "Bohr radius", and tells you the typical size scale of an electron in hydrogen. You could also rewrite this formula in a suggestive way involving the Compton wavelength of the electron:

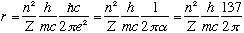
For the velocity, we have

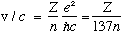
So, v is typically about 1% of c. (If it was much higher, we'd have to go back and worry about relativistic corrections. If Z is big, you must)

Finally, for the energies, we have

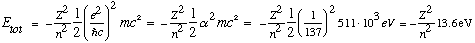
So eV's are indeed the typical energy scale for electrons in atoms.

As an example, an electron dropping from n=2 to n=1 emits a photon with

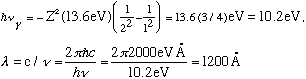
(which is in the UV, a little too short wavelength to be visible)

Bohr noticed that his model not only succeeded brilliantly in many aspects (especially in the prediction of the spectrum), but also yielded what he called "correspondence": at large quantum number, n, the system gives classical results. Bohr found this to be an essential feature - when the system gets big, it should go smoothly into classical results.

E.g., when n is large, the transition from level n to n-1 gives

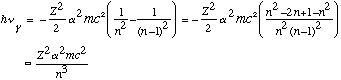
At the same time, the classical rotation frequency for this electron would be

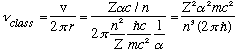
These two formulas match up!

(We will find later that n-> n-2 is not allowed by QM)

Summary of Ch. 1:

(Please read the end of Ch.1 in Gas for many more useful comments at this point)

Classical mechanics + classical E+M fail badly in a number of cases, including

* blackbody radiation,

* photoelectric effect,

* Compton scattering,

* electron scattering off crystals,

* the spectrum of hydrogen,

* and many more...

All of these observations are understood, albeit crudely, if you assume that energy (also angular momentum) is quantized, and if you assume that waves may sometimes act like particles, and vice versa. But, let's be clear: this is still not any kind of framework to work in. We don't know how to compute much else beyond what I've shown you. (E.g., the case of Helium, with two electrons. How do you quantize that??)

Still, at this point, we (and the physicists of the early 20's) are armed with some important ideas to work with

(1) There is a duality between waves and particles, which is given quantitatively by

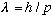
(2) Certain quantities in nature are quantized.

We are almost set up to take the leap to a new mechanics, based on probability waves. It really is a wild leap, and I can't exactlyderive what we're about to do from first principles. But the above ideas should help motivate what we're going to do. Some of the mathematics of waves (and general properties of radiation) will also help guide and motivate the new formalism we want to develop.

So, we need to first examine some of the relevant mathematics of waves, which we're going to be using a lot of. This leads us to Gas. Ch. 2.

(At this point, you might also look at Griffiths Ch. 1.1, and 2.4)