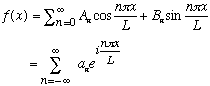
Physics 3220, Fall '97. Steve Pollock.
Here is the Next lecture
Back to the list of lectures
It's hard to think of particles acting like waves. That's why diffraction and interference convinced everyone that light could not be a stream of particles, but must be a wave. But we can think of waves that are "localized". (e.g. a thunderclap, sonic boom, surfer's wave on the ocean) To describe such a "wave packet", we can superpose waves of different frequencies so they add up in one region and cancel elsewhere. This involves the mathematical technique of Fourier Transforms. So, we need to take a math digression, involving a review from 2140 (Boas, Ch. 7, and also 15)
Fourier series were used when we had periodic functions, f(x) = f(x+2L)
For just about any such function, we could uniquely write
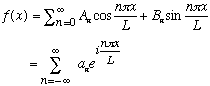
(The two lines are equivalent because of Euler's Eqn,
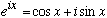 .)
.)
See also Appendix A of Gasiorowicz.
If you are given some periodic function, f(x), there's even a formula to find the coefficients above:
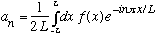
(You can derive this formula if you remember Fourier's "trick", namely
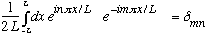 )
)
A Fourier series is, in some ways, like a Taylor series:
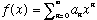 .
.
Here there's also a formula to find the coefficients:
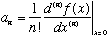
Taylor is "expanding in polynomials", Fourier is "expanding in exponentials"
Both sets (all such polynomials, or all such exponentials) are "orthogonal basis sets" for functions...
We can rewrite the formula for the Fourier series (or Fourier expansion) of f:
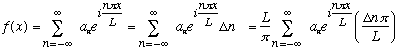
(Delta n is just 1, the difference between consecutive integers)
Now, we define k = n pi/L. (I suppose k should really have a subscript k_n, or maybe an argument k(n). If it's not written it's understood). So we've got:
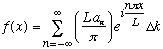
Now define a new function A(k), such that
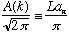 .
(The
.
(The
 is pure convention) What are we doing? How do I ever figure out what A(k) is?
If you give me any number k, I certainly know what n is. (n = L k/pi) And,
given n, I can look up what a_n is. (Or, I use the boxed formula above, which
tells me exactly what a_n is, given n) Then A(k) is known by the little
formula above, A(k) =
is pure convention) What are we doing? How do I ever figure out what A(k) is?
If you give me any number k, I certainly know what n is. (n = L k/pi) And,
given n, I can look up what a_n is. (Or, I use the boxed formula above, which
tells me exactly what a_n is, given n) Then A(k) is known by the little
formula above, A(k) =
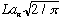 .
.
Rewriting again:
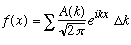
At this point, let L ->
 .
This means f(x) is no longer periodic! It also means, since k = n pi/L, that
the k's are getting very close together. k is becoming a "continuous variable".
In this limit, the sum above becomes an integral,
.
This means f(x) is no longer periodic! It also means, since k = n pi/L, that
the k's are getting very close together. k is becoming a "continuous variable".
In this limit, the sum above becomes an integral,
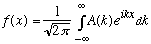
This expression is called a Fourier transform. Or, we might say f(x) is the Fourier transform of the function A(k). We wrote down the formula for A(k) above, let me rewrite it (bearing in mind this limit L -> big):
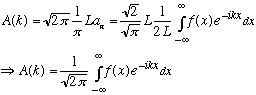
This last expression is sometimes called the inverse Fourier transform, or we might say A(k) is the inverse F.T. of f(x). Note a little bit of remarkable magic: the formula for A(k) in terms of f(x) is almost identical to the formula for f(x) in terms of A(k) (except for the sign in the exponential). For this reason, we may get a little sloppy and leave out the word "inverse", i.e. we just say "A(k) and f(x) are Fourier transforms of each other". (It didn't have to be this way, but it's very handy that it works like this. )
The bottom line is, if you give me any (reasonable) function f(x), even if it's not periodic, I can perform the (nasty) integral above, which gives me a new function A(k). A(k) is completely different from f(x), but it is intimately connected. If I know A(k), I can find f(x) just by doing an integral, and vice versa. In a certain sense, A(k) and f(x) are partners in life. If you know all about one, you immediately know all about the other. They carry equivalent information content. I can think about "the function in x" or "the function in k", whichever is simpler.
We can even have some physical interpretation for A(k) (which is a lot like the
interpretation of the coefficients in a Fourier series). Roughly
speaking, any function f(x) can be thought of as a superposition of an
infinite number of simple waves. (That's what the integral is, think of it as a
sum over all possible plane waves). Each wave has wavelength
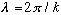 ,
and A(k) is the amplitude of that wave. If A(k) is big, it means you
need to include a large amount of plane wave with that particular wave number.
If A(k) is small, you don't need to add any waves of that wave number. If I
suppose, for simplicity, that A(k) and f(x) are real, it's especially
transparent:
,
and A(k) is the amplitude of that wave. If A(k) is big, it means you
need to include a large amount of plane wave with that particular wave number.
If A(k) is small, you don't need to add any waves of that wave number. If I
suppose, for simplicity, that A(k) and f(x) are real, it's especially
transparent:
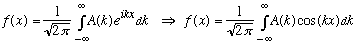
The latter formula really looks like a superposition of a bunch of ordinary sin (here, cos) waves, with amplitudes (or "strengths") given by A(k).
Example:
Suppose I sum up a bunch of plane waves, and the strength, or amplitude, of the plane wave with wavenumber k is given by
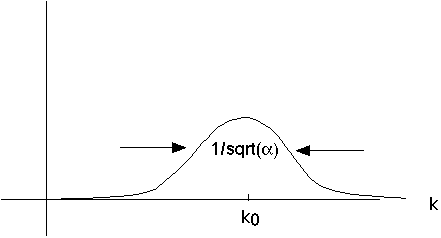
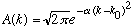 .
.
This is just a Gaussian, centered at k0. (So, I'm adding up all plane waves, but mostly I'm going to use wavenumbers near k0, tailing off for wavenumbers on either side)
Now, if I sum up plane waves, with amplitudes as given by A(k), what does the resulting wave packet look like? That's f(x):
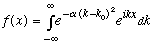 We can do this integral.
We can do this integral.
First, rewrite k x = (k-k0) x + k0 x, giving
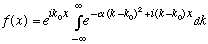
Next, shift the integration variable, i.e. define k' = k-k0 (dk' = dk, still)
Also, observe that
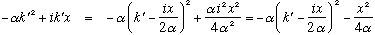 ,
,
an algebra trick known as "completing the square". This is still the argument of the exponential in the integral, but the second term is independent of k', so comes out of the integral. If we shift variables again, now letting
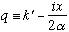 (again, it's just a constant shift, so dq = dk' still), leaving:
(again, it's just a constant shift, so dq = dk' still), leaving:
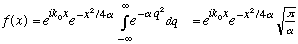
That's our answer. It is simply a Gaussian function in x. (There is a complex phase out front, which makes it look more complicated, but it's irrelevant if you take |f(x)|^2, which it turns out we'll most often be interested in, in QM)
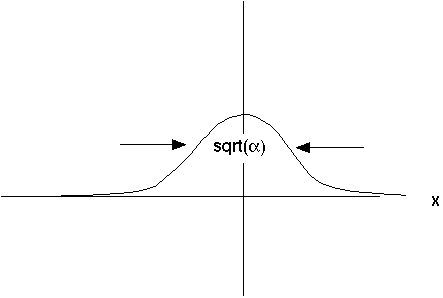
f(x) looks a bit like a "particle", or at least like a localized disturbance centered at the origin. Because f(x) is not real, we might even want to argue that |f(x)|^2 is better to think of as the "particle".
It's an essential observation that the width of A(k), which we call
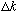 ,
is approximately 1/
,
is approximately 1/
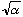 ,
whereas the width of f(x), called
,
whereas the width of f(x), called
 x,
is about
x,
is about
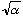 .
.
The product of
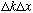 is roughly unity. This is not just an accident of this particular example. To
build a "particle" (or a wave packet, f(x)) with some given size, you need to
superpose many different wavelengths. How many? You need to span a range of
wavenumbers which gets larger, if you want to localize your particle better. It
turns out, purely mathematically, that
is roughly unity. This is not just an accident of this particular example. To
build a "particle" (or a wave packet, f(x)) with some given size, you need to
superpose many different wavelengths. How many? You need to span a range of
wavenumbers which gets larger, if you want to localize your particle better. It
turns out, purely mathematically, that
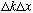 is greater than 1, but is of order 1 for many "packet-like" shapes. It doesn't
really matter what the exact functional form of A(k) or f(x) is.
is greater than 1, but is of order 1 for many "packet-like" shapes. It doesn't
really matter what the exact functional form of A(k) or f(x) is.
This purely mathematical fact has very important consequences in Q.M.
A homework example is rather similar:
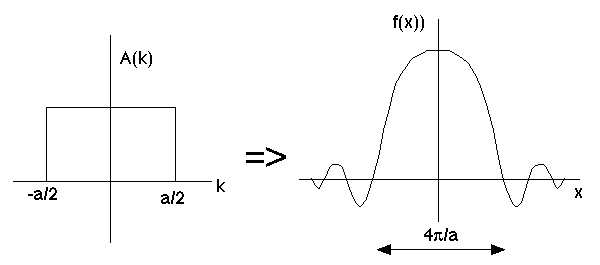
Again, we see the widths are roughly inverses of each other. (Our "order 1" in this case is about 4 pi!)
(Does this picture remind you of light waves going through a square slit...?)
| list of lectures | 3220 main page | Prof. Pollock's page. | Send comments |