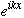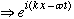Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 2, lecture 5 (Fri 9/5/97)

Here is the Next lecture

Back to the list of lectures

Let us first try to generalize our plane wave, 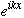, to include time variations, .

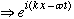If the wave were a simple light wave, then .

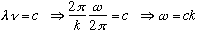So for light, the full space and time dependence for a given frequency (or wavenumber) is .

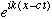If you now build up a packet by summing many different wavenumbers, i.e.

,

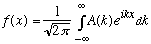and you let each wavenumber have its correct time dependence, you get .

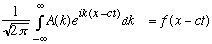The shape does not change, you just find a traveling wave packet, with v=c.

In general, for most waves (water, or even light in real media), 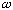depends on k. This is called dispersion. So, more generally,

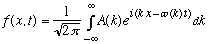
This integral is hard to analyze in full generality; let's begin by looking at the same Gaussian example we had before, 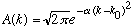. (This Gaussian will become our favorite wavepacket, because it looks like what we think a particle should look like, and it's mathematically tractable. It has many nice properties, and forms a good starting basis for real life problems)

We're going to make a simplifying approximation: let me assume 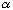is fairly big, which means that only values of k very close to ko will matter. (big alpha means that A(k) is narrow).

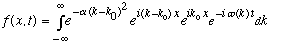
Since alpha is big, the leading term means that the only places the integrand is of reasonable size is right near k=k0. I can Taylor expand 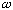(k):

.

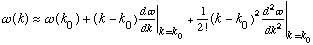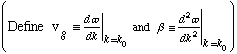
v_g is called the group velocity, we'll see why shortly.

We plug this expanded, approximate form for 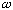(k) into the integral, change the integration variable from k to k'=k-k0 (so, dk' = dk), and get

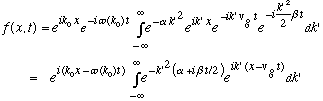
The integral in the 2nd line is exactly the same one we did to find f(x) in the previous example. The only differences are:

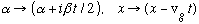
The old answer we got was , which means our new answer is

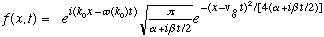
It's correct, but not very intuitive yet. (Note that Gas has made typos in his eq's 2-15 through the rest of that section - you should replace his "beta" with "beta/2" everywhere...)

Remember last time I argued that it's |f(x,t)|^2 which will really end up representing the physical particle:

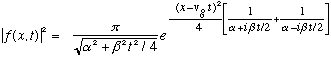
The argument in square brackets, in the exponential, equals .

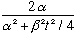The amplitude is out front. It slowly shrinks with time. (Remember, alpha is big) It appears to be, roughly, a traveling wave packet that looks like a Gaussian, and it travels along at v_g. (Since the whole packet travels along with velocity v_g, we call this the "group" or "packet" velocity)

The width of the packet is changing with time, and is given by

.

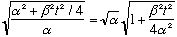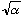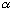At t=0, it starts out with width (we knew that from the previous example), and it gets wider as time goes on. The smaller is, the more rapidly it spreads out. A particle which is initially fairly well localized in space will travel along, with velocity v_g, and spread out. The more well localized it initially is (smaller 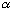) , the faster it will spread out.

Making wave packets into particles

We want this wave packet to somehow represent a particle, that's the game we're playing. This particle should be as classical and pointlike as we can make it: it should have momentum p, and energy E = p^2/2m. (we'll be sticking with nonrelativistic particles throughout this course)

We already saw that such a packet moves with velocity 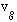, i.e. .

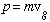We will also want to make the "quantum ansatz" of Planck and Einstein that 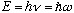, i.e. .

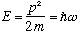We just stated that 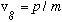, and above we had defined

.

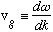Thus,

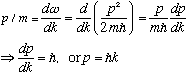
We have gotten DeBroglie's relation back, which is a good thing. In other words, building up wave packets to look like particles automatically generates DeBroglie's relation.

Now we go back and rewrite our original relation

,

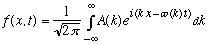making use of what we just got (i.e. rewriting k and 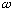in terms of p and E):

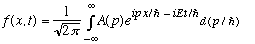
We're going to do some (slightly inobvious) manipulations, at this point purely formal, to see a very important result about this f(x,t). (We will take certain partial derivatives of f with respect to t and x, and notice a connection:)

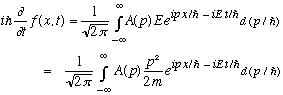
whereas differentiating with respect to x (twice) gives the same thing:

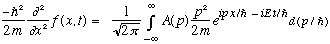
Let's put this all together:

If we insist only that our time dependent wave packet should represent a particle with energy 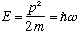(no potential!)

and with momentum ,

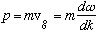then we have found quite generally that 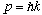, and also that the wave packet satisfies the equation

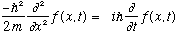
which is Schrodinger's Equation!

We have not proven anything, only demonstrated that building wavepackets, (asking that we make particles out of waves) while satisfying the classical 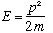and the quantum 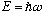leads to Schrodinger's Eq'n. We'll come back again and see this in other ways soon...

Uncertainty relations

Recall what we learned for our evolving wave packets. First of all, ,

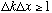the width in space goes inversely as the spread in wavenumbers. (I will define what 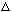means more rigorously soon enough) So, using DeBroglie,

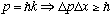, the (in)famous Heisenberg uncertainty principle. This means that if you try to build a localized wave packet in space, it cannot have a well defined momentum. (That's because you have to sum over many different plane waves of different k's to built a narrow packet)

We try to impose classical concepts like position and momentum on particles, but for wave packets you really cannot do this. Classically, p and x are independent. But Q.M. says they are connected, they are complementary aspects of one system. Read Gas. pp. 33-36 for a nice discussion!

Fortunately, Planck's constant is so small, you ordinarily don't care or notice.