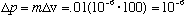Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 2 (and starting Ch 3), lecture 6 (Mon 9/5/97)

Here is the Next lecture

Back to the list of lectures

Example: A mosquito has m = .01 g, and velocity v=100 cm/s. Suppose its velocity is constant, and measured to 1 ppm (!) Then,

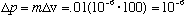g cm/s

Thus 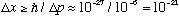cm, immeasurably small.

Apparently the uncertainty principle just doesn't matter for even quite small objects.

(If you go back to our spreading wave packet, and look at the spreading of wave packets with time, Planck's constant is so small that this spreading never matters for finite times for normal sized objects. )

However, if you are looking at an electron in an atom, then

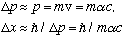
which is the Bohr radius. (The electron is essentially delocalized througout the hydrogen atom)

Using uncertainty to make predictions (!)

Amazingly, is not just a "negative statement", because often for quantum systems that > sign turns into an = sign. This allows very nifty (quick and dirty) estimates of QM sizes, and other quantities. You have to be careful about these arguments, but in many cases they work fine...

For example, consider again the hydrogen atom. We know that

.

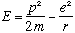The uncertainty principle tells us ,

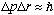and it seems reasonable to assume here that ,

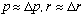(do you see why? Think of an electron running around in the atom. It has a momentum of some magnitude, but it is pointing in different directions as it runs around in circles. You might think of the uncertainty in the momentum here arising from the uncertain direction of travel. Also, the electron is surely found somewhere in a sphere of radius r, but it could be just about anywhere. So, the uncertainty in position is roughly the same as the size of the system. This is not always true, that 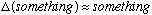, but often is - you must think about the problem to decide if it seems reasonable.)

In any case, combining the last three expressions gives us

.

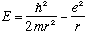If we want to know the ground state, E is minimized,

.

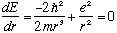Solving this gives 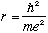which is the Bohr radius, about half an Angstrom!

Also, plugging this radius back in to our formula for E, 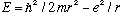, gives E=-13.6 eV, the correct answer.

There really is some physics here - you could imagine trying to lower the potential energy of a hydrogen atom by bringing the electron in closer, binding it more deeply. Classically, you could do this, and indeed the electron would spiral in. But, the uncertainty principle says that by making the radius smaller, the momentum would have to grow, and thus the kinetic energy would increase. There's a balance, and that gives the radius.

Another example:

A deuteron is a bound state of a proton and neutron, and has size about 1fm (= 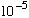A). What sort of binding energy do you expect this object to have?

The nucleons (p and n) must obey the uncertainty principle, .

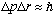So in this case, .

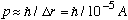The kinetic energy of the nucleons must be

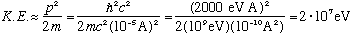
This is a positive energy. To be bound, the potential energy must be at least this big. Indeed, the binding energy is experimentally found to be this order of magnitude.

This gives us the beginnings of ideas about wave-particle duality, and some of the consequences. Next, we will start from the differential equation we "derived", and just treat it as a postulate, making some guesses as to the interpretation of the equation, and this "wave packet" f(x,t).

Gas Ch. 3: The Schrodinger Equation, and Probability Interpretation

.

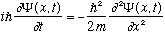Recall what we discovered in Ch 2; namely, the function

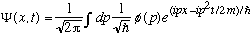
always works (i.e., it satisfies the S.E.), no matter what the function phi(p) is! (Before, we called the left hand side f(x,t), and here I've let .)

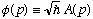(You might ask, does this equation generate all possible satisfactory 's? The answer is yes, but we won't prove it.)

(You might also ask if, given 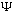, is phi unique? Again the answer is yes - this is a property of Fourier transforms.)

You should note that because of the complex exponential, 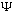is itself in general a complex function, not a real function!

The S.E. is linear and first order in the time derivative. This means:

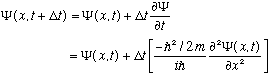
So, if you give me the complete function 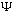(x,0), I can immediately find 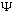(x,t) for any other time, t. The time evolution is simple, given the S.E. Alternatively, if you give me some valid 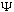(x,0), which is given by the (unique) expression:

,

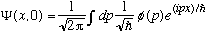then I could "inverse Fourier transform" this expression, and derive

.

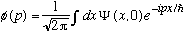(I'll work out the details shortly, to show all these coefficients are right!). Once I know phi(p), I then use the boxed equation at the start of this section to find 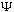(x,t) The bottom line is that you only need to know phi(p), or 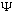(x,0), and then you know the wave packet for all other times!

What exactly is this "wave function" ?

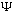We've been calling it a wave packet, but what exactly does that mean?

Max Born (1926) suggested that 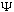is a mathematical function associated with the presence of a particle, and that the probability of finding the particle somewhere between (x, x+dx) at time t is given by

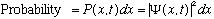
Normalization of probabilities requires (the particle must be somewhere)

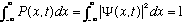
We will soon show that if the above is satisfied at time t=0, (and if 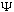is even mildly well behaved), then it will stay satisfied forever.

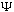may "spread" out, or wiggle, or do whatever the S.E. tells it to do, but the particle doesn't begin to disappear, nor do new ones spontaneously appear. (We say that a 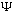satisfying this integral equation is "normalized")

The S.E. is linear, which means that if 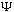1 and 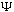2 are solutions, then so is the linear combination 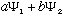, for any constants a and b. (They can even be complex). This result may not be normalized, but since c( 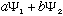) will also be a solution, then you can always pick c to properly normalize this result.

If 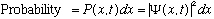, do you suppose we will ever care about the complex phase of the wave function? (Since we square it anyway to find probability, can the phase be observed?) The answer is a qualifiedyes. In particular, you do care about phases when you form linear combinations.

Suppose for example that 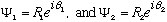. You might think that the 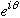's are irrelevant, since they vanish upon squaring. But, suppose we need to add these solutions, and ask about the probability then?

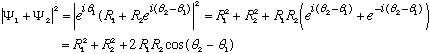
The phases do appear in the result! Technically, then relative phase matters (but indeed the overall phase really doesn't matter in the end.)

By the way, the cosine or "interference" term is exactly the same as what gives you the familiar interference pattern in 2-slit experiments (where you also add complex fields.)

Next time, we will prove the statement I made above, "conservation of probability":