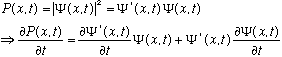
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 3, lecture 7 (Wed, Sept 10, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Let's now prove the statement I made at the end of last time, "conservation of probability":

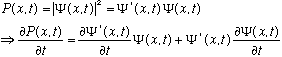
But, the S. E. says

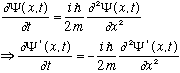
Combining with what we had at the top, i.e replacing time derivatives with second order spatial derivatives yields

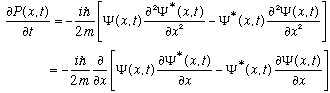
The second line you have to check! (It turns out that "x" derivative introduces some extra pieces 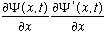, but they fortuitously cancel out)

We define the object being differentiated above to be a new function, -j(x,t), i.e.

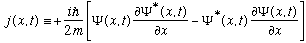
(Note the sign!) So a summary of what we've just found is

.

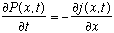If you now integrate both sides of the above equation over dx, you find

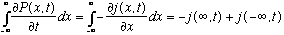
Because our wave function is square integrable, it must vanish at infinity (as must its first derivative), which means that j(x,t) must go to zero at infinity.

Thus, the right hand side is zero, and so

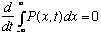
The probability integral is independent of time, which is what we set off to prove! (If it equals 1 at some time, t=0, it equals 1 for all other times)

What exactly is this j(x,t) function? It has an important and fairly "physical" interpretation, which we can understand by going back a step. Instead of integrating over dx from -infinity to infinity, just integrate from "a" to "b":

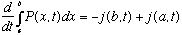
The left hand side is the change in probability of finding a particle somewhere between (a, b), with time. That is, it tells you how much "particle" is entering the region (a,b) per unit time. So, j(x) must represent how much "particle" is passing by the point x, i.e. the flux, or current of probability.

You've probably seen derivations and equations very much like the above in E+M, only there instead of "probability density", you were talking about "charge density", and so instead of probability current, you found charge current. (This equation is simply an expression of the conservation of charge.)

The above was all in 1-D. To write this in 3-D, replace .

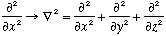Following through exactly as above, you will find:

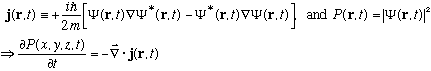
Even if we were to add an extra term, 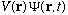to the right side of the S.E., this would not affect the equations above at all (as long as V(r) is real), because

we will simply add and immediately subtract a term in j that looks like 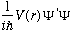. (you should verify this statement)

If you have a wave function Psi(x,t), and the corresponding probability P(x,t),

you can form something called the "expectation value" of x, or "average value":

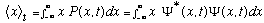
The meaning of this quantity is a little subtle: If you have many identical systems (all in the same identical wave function, psi(x)) and you measure "x", the position, of the particle in each, you will find different values in the different systems. The above is the average of what you will find. Not that this does not mean that if you keep measuring x, it will flop around, and you form an average that way! (As we will see, measuring x changes the wave function, in general!)

For future reference, we can find the expectation value of any function of x, not just x alone, and the definition will be

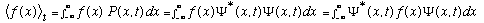
What about the expectation value of momentum? I suppose you might suspect that we should just write down

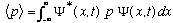? But this doesn't really make any sense, because p isn't a function of x (at least, classically, they're independent), so you could pull the p out, and this equation would be meaningless)

Since the wave function depends on time, it should be clear that <x> can too:

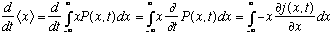
Next time, we will find the average value of momentum by "m v", where v will be the time derivative of the average value of position.