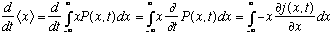
Physics 3220, Fall '97. Steve Pollock.
Here is the previous lecture
Here is the Next lecture
Back to the list of lectures
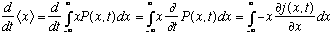
We can integrate the last expression by parts, giving
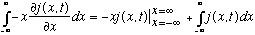
The first term on the RHS vanishes (as we discussed before, j vanishes at infinity (there's no "current" way far away from where the action is!) The remaining term can be evaluated by plugging in the definition of j(x,t),
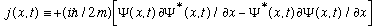 ,
,
so we have
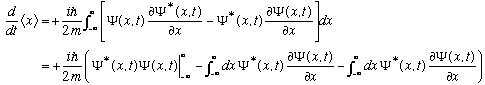
(The 1st 2 terms in the last line arise by integrating the 1st term in the line above by parts. The last term I just carried straight over from the line above.)
Rewriting, again noting that Psi vanishes at infinity:
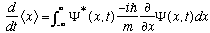 .
.
I would expect, naively, that the time derivative of the average position should give me an average velocity, or
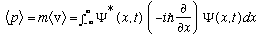
We will use the real expression for <p> we just got, to write down the following extremely important formula:
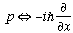 ,
,
i.e. we will think of momentum as an operator in quantum mechanics!
(Sometimes, to remind ourselves, we'll call it
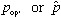 ,
or p)
,
or p)
As before, we can find expectation values of functions of momentum:
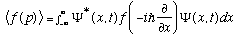
So, e.g., if you wanted to know the expectation value, or average value, of kinetic energy for a particle with a wave function psi, you would compute
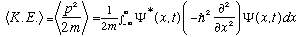
Let's now go back to that function phi(p), and think about it some more. Recall:
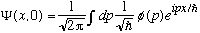 .
.
Remembering that p=
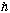 k,
this means
k,
this means
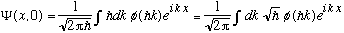
This is a Fourier transform, and we learned how to invert them:
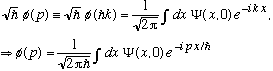
The last line provides us with a formula to find phi(p), given Psi(x).
Note 1:
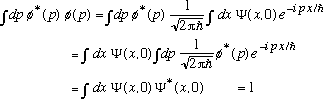
If Psi(x) is normalized, then phi(p) is also. (This is "Parseval's theorem")
Note 2:
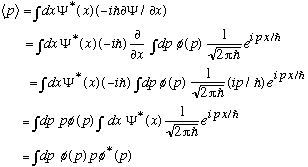
It really looks like phi(p) is some sort of a wavefunction, just like Psi(x).
It is normalized, and the expectation value of p "in momentum space" looks just
like the expectation value of x did in "position space". This last equation
implies that the probability to find momentum between
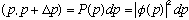 .
.
It is also true (though you must prove it, in a manner much like note 2) that
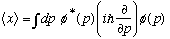
So, "in momentum space", x is an operator.
"In position space", we already saw it was p that was the operator. And, the form of the operator is very similar (note the sign flip, however.)
Adding a potential
So far (for free particles), we've been using the S.E,
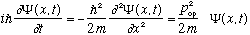 .
.
Given the results of Ch. 2 (where we saw that
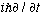 pulled down the total energy of the wave packet) it might be intuitive, or at
least somehow reasonable, to postulate that when there is a potential
energy present, the kinetic energy on the right hand side should be
replaced by the total energy, kinetic + potential, i.e.
pulled down the total energy of the wave packet) it might be intuitive, or at
least somehow reasonable, to postulate that when there is a potential
energy present, the kinetic energy on the right hand side should be
replaced by the total energy, kinetic + potential, i.e.
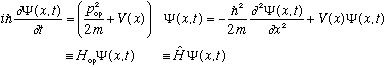
H is the Hamiltonian, the operator version of the classical H, which gives
H= total energy = Kinetic + potential.
We will use operators all the time in quantum mechanics, and here and in the
next chapter we will spend some more time discussing what operators are and how
they work. (In a sense, "x" in position space is also an operator, but it's a
rather trivial one, it's the "multiply by x" operator:
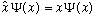 )
)
| 3220 main page | Prof. Pollock's page. | Physics Dep't | Send comments |