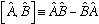.Physics 3220, Fall '97. Steve Pollock.
Here is the previous lecture
Here is the Next lecture
Back to the list of lectures
We can define the commutator of two operators A and B:
.
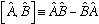Why isn't this zero? Well, sometimes it is, sometimes it isn't. Remember that operators must always operate on something! So, to analyze any operator, you must let it operate on a function.
Ex. 1: (A zero commutator)
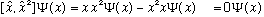
Since we get zero no matter what psi is, the commutator is indeed zero. BUT
Ex. 2: (A nonzero commutator)
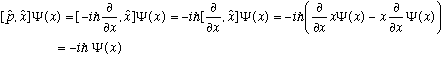
Since this expression is true no matter what Psi is, we say
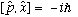
(The right hand side is here an operator, the "multiply by -i hbar" operator)
It's pretty bizarre that a commutator could be nonzero, and this particular one will lead us to the uncertainty principle - we'll see how later.
I remind you that in position space,
.
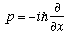But wait a minute - what's that "i" doing there. Isn't momentum real??
Not to worry. Consider for example
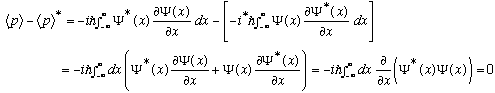
Which means <p> is real! It looks imaginary, but in the end, expectation values are real. Note that I didn't have to specify Psi, this expectation value is always real no matter what Psi is! Such an operator is called Hermitian.
(It's very easy to show that the operator x is also Hermitian).
If a generic operator A is Hermitian, then <A> = <A>*, which means that
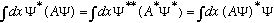
(No matter what A or Psi are) Gas, in his Appendix B, uses a math trick to prove that if this the case no matter what Psi is, then it must also be true that
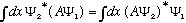
So Hermitian operators can act on either wavefunction, Psi1 or Psi2, it doesn't matter. They can "act rightwards" or "act leftwards", they're very friendly operators.
Summary of Gas chapter 3:
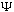is a wave function, what we called a "wave packet" before. It is not really the
same as the particle, it is a mathematical probability amplitude. (The particle
is not "made of waves", but the wave function (Psi) describes the
particle.)
Intepretation of Psi:
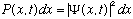= the probability to find the particle between x and x+dx.
Psi satisfies the Schrodinger Equation:
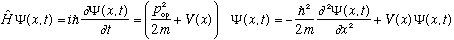
Given Psi, you can also find another (related) function, phi, which we call the "momentum space wave function:"
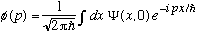
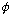(p)
is essentially equivalent in information content to
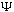(x).
It is normalized, and
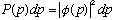= the probability to find the particle with momentum between p and p+dp
In quantum mechanics,
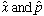are really operators, not numbers, and explicitly
.
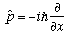The operators p and x do not commute, but rather
.
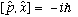Let's discuss operators further. Our generic operator will be O
(or
)
O must always operate on something, in our case often on a function.
It will always give back something of the same type (again, a function).
There are many operators, and they can have very different characters. Here are some random examples:
Operator symbol Instruction Example
3 multiply by 3 3 f(x) = 3 f(x)
d differentiate d f(x) = df(x)/dx
c complex conjugate c f(x) = f*(x)
k destroy k f(x) = 0
An important class of operators are linear. If L is linear, this means the following 2 things:
1) L [f1(x)+f2(x)] = L f1(x) + L f2(x).
(So e.g. the operator "squared" does not satisfy this condition, but all the examples above do)
2) L c f(x) = c L f(x), where "c" is any constant, even a complex constant.
(3 and d and k above satisfy this condition, but the c operator above does not.)
We will start thinking about functions as analogs of a vector, soon. How so?
Consider a normal 3-vector,
.
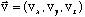You can easily imagine generalizing this to an "n" dimensional vector,
.
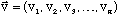This is a collection of values, vi (each value is labeled by an
integer i). If you let n go to infinity, you're thinking of some object with
an infinite number of values associated with it. This is basically what a
function f(x) is. You can think of it as a collection of values f(xi),
and each value is labeled by the (real) number xi.
(The analog of
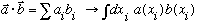
You can also consider operators that operate on vectors, and give back some
other vector. For example, you could consider the operator called
,
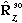which operators on a vector, and rotates that vector about the z axis by 30
degrees.
(We may further specialize to the world of unit vectors, so R only operates on unit vectors. If you think about what R does, it also always returns a unit vector. Unit vectors are an interesting subspace of all vectors. The analog, in the world of functions, might be functions that are normalized to one!)
For some operators, there are some magic or special functions (vectors) f, such
that
,
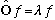where
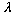is simply some number. Operating on this special object gets you back exactly
what you started with, or at least proportional to it.
The special function f is called an eigenfunction (or
eigenvector) of O, and
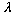is the corresponding eigenvalue.
Example 1. (vector operator)
The vector operator
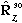has only two eigenvectors. They are
,
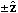and the eigenvalue in both cases is +1. (Convince yourself that all
other unit vectors, rotated by 30 degrees, give back a unit vector which is
not proportional to what you started with! )
Example 2. (function operator, boring)
The operator 3 defined in our table above has lots of eigenfunctions. In fact, all functions f(x) are eigenfunctions. And they all have the same eigenvalue, 3.
Example 3. (function operator, less boring)
Consider the operator d from the table above, d = d/dx. Does it have any eigenfunctions? If it did, that would mean that
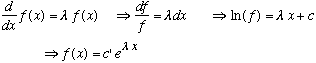
So such functions do exist - exponential functions. Only exponential functions are eigenfunctions of this operator. The coefficient of x in the exponential is the eigenvalue. This is a special limited class of functions, but it turns out you can get any eigenvalue you want (all complex numbers).
As we have seen, eigenvalues can be discrete (Ex. 1 and 2 above), or continuous (Ex. 3 above).
Remember in the last chapter we found a most important operator, momentum
.
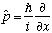We just did all the work we needed to in Ex. 3 above, and have found that the
eigenfunctions of momentum are exponential functions of the form
.
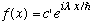(The eigenvalue is then
).
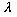But this symbol is just a dummy.
I could have called it by any name I want. For obvious reasons, we
usually call the eigenvalues of the momentum operator "p". The
eigenfunctions of momentum are called
,
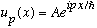and we have
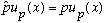
There is a perturbing proliferation of "p"'s in this perplexing equation.
The first one is the momentum operator (which we could have written in its derivative form if we'd wanted) Next there is the subscript on the function name, u_p. I didn't need to put it there either, but it reminds me that this particular function u_p is an eigenfunction of momentum, with particular value p. The third "p", right after the equals sign, is the value of the momentum. It is simply a number, NOT an operator anymore. It is the number which appears as the coefficient of x in the exponent of u_p(x).
Let's look back at the Schrodinger Equation:
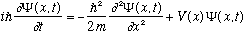
(Note that I've picked a potential, V(x), which depends only on position, but is not varying in time. Time dependent potentials certainly do exist, but the form above is pretty general, and we'll stick with it most of this semester.)
This is a partial differential equation ("PDE"), and as you must have noticed by now, we always try to solve PDE's by the technique of separation of variables.
This means we guess that the solution is of the form
,
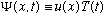and plug back into the Schrodinger equation, giving
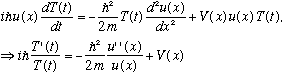
(The second line comes from dividing the first line through by "u(x)T(t)")
But this last expression is crazy! How can a function of time = a function of space? It's completely impossible, unless it so happens that neither side is really a function of anything, i.e. both sides are a constant. We give this constant a name, totally arbitrary for now, say "E". This means we really have two equations, one for the function of time, one for the function of space.
Next time, we will solve the the first equation (the time one). Today, just look at the second equation (for the space part):
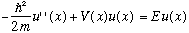
This is an eigenvalue equation, just like we talked about at the start of this section. (That's one reason we spent some time talking about operators and eigenvalues. This equation is so central to quantum mechanics!)
The operator in this case is
.
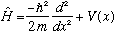The first term in this operator is a "double derivative" operator, and the second term is a "multiply by V(x)" operator.
We could also write
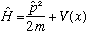(in terms of the momentum operator)
Using this notation, we can rewrite our differential equation so it more obviously looks like an operator eigenvalue equation:
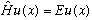
Solving the S.E. amounts to trying to solve this eigenvalue equation. That means trying to find all possible eigenfunctions u(x), and also trying to find all possible eigenvalues, E.
Puzzler, to end this lecture:
Consider the operator x, which is defined in the usual way, x f(x) = x f(x),
it is the "multiply by x" operator. As usual, I can ask, "what are the eigenfunctions of this operator?" Mathematically, I am asking to find f(x) s.t.
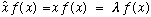
That's an awfully funky looking equation. Remember that
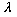is supposed to be a constant. But, the equation is an equation,
i.e. it must be true for all x if it's to be a true equation! At first
glance, you might say it's absolutely impossible to ever solve this equation.
(You might notice that f(x)=0 is a solution, so "zero" is certainly an
eigenfunction. But it's also rather trivial, and exceedingly dull.) But, there
is another more interesting solution! That's the puzzle.
| 3220 main page | Prof. Pollock's page. | Physics Dep't | Send comments |