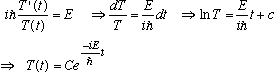
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Chapter 4, lecture 10 (9/17/96)

Here is the Next lecture

Back to the list of lectures

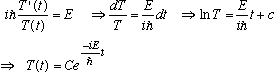
I have found the solution, quite independent of V(x), for the time dependence of the wave function! (I hinted at the start of the previous chapter that the S.E. is like that - once you know the wave function at some time t, the wave function at other times is pretty simple. Bear in mind that I'm not really done yet - with the method of separation of variables, you may find that the solution you get is not general enough, and you might have to superpose solutions. We'll get to that.) Also, if V=V(x,t), all bets are off, and life is tougher.

We are still left with the other equation, for the space part, which we discussed last time:

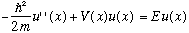
This is an eigenvalue equation, just like we talked about at the start of this section. The operator in this case is .

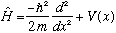We can rewrite our differential equation so it more obviously looks like an operator eigenvalue equation:

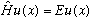
Solving the S.E. amounts to trying to solve this eigenvalue equation. That means trying to find all possible eigenfunctions u(x), and also trying to find all possible eigenvalues, E.

Since eigenfunctions and eigenvalues go together, I will often add a label to the function u(x), i.e. I will give it a slightly more descriptive name than the minimalist "u(x)", and so I might write

.

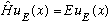In general, as discussed above, eigenvalues can either be continuous or discrete. If the eigenvalues E are discrete, I might label them by an integer n, and say .

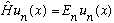We say "u_n(x) is the eigenfunction of H corresponding to the eigenvalue E_n"

Because the S.E. is linear, we can always superpose solutions. This means that a completely general solution to the S.E. will look something like this:

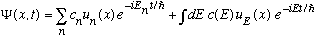
I sum over discrete eigenvalues, and integrate over continuous ones, to get them all. The c's above are basically arbitrary. Different sets of c's give me all different possible Psi's that solve the S.E. (I might pick a particular set if I have some boundary conditions that Psi must satisfy.)

There is one important extra condition, however: we must insist that our wave function always be normalized, because of Born's probability interpretation:

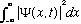=1.

Math Interlude: Delta Functions

Definition #1. (Don't show this to a mathematician, but...)

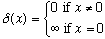
subject to the additional condition that

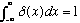
(Technically, the "delta function" is not really a function, but physicists pretend it is anyway, and we seldom seem to get into trouble for it)

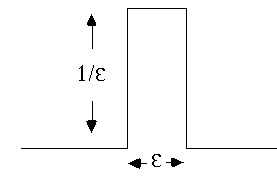
I'm uncomfortable with that infinity symbol in the definition; I like to think of this function as a limit of functions that look like this, in the limit that 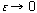(they're getting narrower and narrower and higher and higher, but always with unit area) In the limit, you have a delta function.

By the way, although my narrow spiky function was square, it doesn't have to be. You could use any narrow spiky function normalized to 1. E.g, just as good:

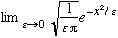
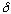(x-a) is just a delta function centered at the point x=a. What if you take such a delta function, and multiply it by a normal function f(x)? When x differs from a, the delta function vanishes, and you get zero. When x=a, the delta function blows up, but f(x) is being evaluated at x=a. So you get

f(a) 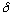(x-a). This means that

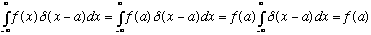
This is what delta functions DO. They pick out f(a) for you.

Definition #2.

For this definition, which turns out to be equivalent, though very different looking, we need to think a bit about Fourier transforms again.

,

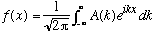and the inversion of this formula tells us A(k),

.

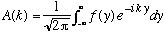(I changed dummy variables in that integral to y, you'll see why)

Now, take the second equation, and plug it right back into the first one!

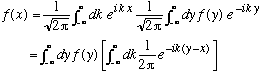
I am going to take the "inner integral" in brackets in the second line, which is manifestly a function of both x and y, and give it a name, delta(y-x), i.e.

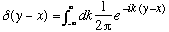
What I just showed was that

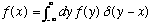, or (replacing dummies "x" with "a", and "y" with "x' ")

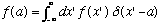
Exactly the same result as I had above. So, this "Fourier transform" definition of a delta function gives me something which acts just like I want a delta function to act - it plucks out a value of a function at a single pt.

It appears I have several different ways of thinking about delta functions. It's a narrow spiky function with area 1, or it's defined by the formula

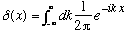
or, I could just define it as the function which always yields the result

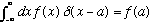for any function f(x). They're all basically equivalent.

The Fourier type definition is probably the most unfamiliar to you. Maybe I can make it at least vaguely reasonable in the following sense. If k is not zero, then the integrand wiggles, and the area under such a wiggling curve vanishes. (The real and imaginary parts are just cos(k x) and sin(k x), the area under each of which is zero) But if k=0, then I just have the integral over dk, which blows up. So this odd definition does appear to have the property of being zero everywhere except k=0, and then blowing up at k=0. (The unit area aspect is really what we worked out on the previous page.)

The delta function has several other important properties we will use, e.g.

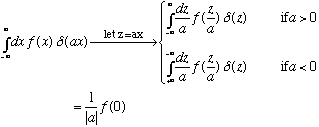
Or in other words,

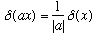
Example: What is delta(x^2-a^2)?

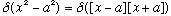. This gets "spiky" at two points, x=a and x=-a.

When x=a, what we have looks like

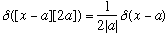
When x=-a, what we have looks like

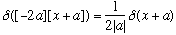
Putting this together we have

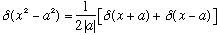
By the same logic as the previous example, here's a much more general result:

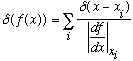
where 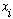is a root (or zero) of f(x).

What about ?

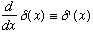We can figure out what this is by integrating by parts:

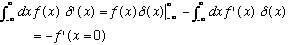
These rules are most of what we'll need to work with delta functions.

Now, finally, we can return to the eigenvalue puzzle I set up a few pages back,

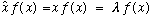
The answer, by inspection, is that f(x)= 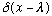. Why is this so?

If x is different from 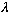, then both sides of this equation give zero.

If x= 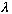, we have already seen that .

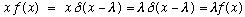So, no matter what x is, the equation is satisfied!

(It makes some sense, the eigenfunction of x should be a function that somehow has a single, definite value of x, just like the eigenfunction of p was a function that somehow had a single, definite value of p.)

Summarizing,

The eigenfunctions of p are plane waves, ,

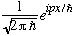The eigenfunctions of x are delta functions, .

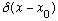Just as an aside, notice that these functions are basically just Fourier transforms of each other:

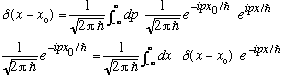
We leave this long delta fn interlude, and return to our discussion of the S.E.

A classic eigenvalue problem: Particle in a box.

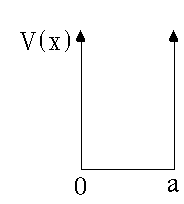
Suppose the potential looks like this, it is zero for x between 0 and a, and infinite outside. (This is a "box", with no force at all as long as you stay inside, but infinite force if you hit a wall) It's a one dimensional version of a pool table. As always, the S.E. is

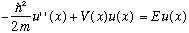
(Recall, we have already separated out the time dependence a few pages earlier.) u(x) must remain finite everywhere, otherwise it could not have a (finite) norm of 1. When x<0, or x>a, V(x) is huge (infinite), and if u(x) was anything besides 0 there, we would have an equation that had two finite terms (the first on each side) and one infinite one (the V(x) u(x) one). That's no good, so it better be the case that u(x) vanishes everywhere "outside the box". It's also a generic requirement for wave functions, u(x), that they be continuous functions. (Otherwise, the second derivative is not even defined). So, that means u(0) = u(a) = 0. Next time, we'll solve the S.E, and find the rest of u(x)!