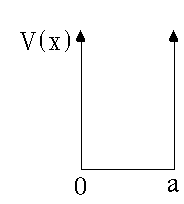
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 4, lecture 11 (9/19/96)

Here is the Next lecture

Back to the list of lectures

The classic eigenvalue problem: Particle in a box.

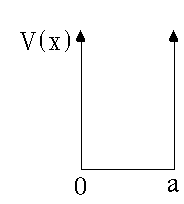
We are solving S.E. with this potential: it is zero for x between 0 and a, and infinite outside. The S.E. is

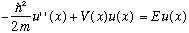
As discussed last time, u(x<=0) = u(x>=a) = 0.

(The particle must not be allowed outside of the box, and u must be continuous)

Inside the box, V(x) = 0, so for 0 < x < a, the equation we're trying to solve is

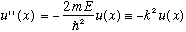(This equation defines the constant "k")

This is an eigenvalue equation, subject to the extra condition u(0)=u(a)=0.

It's a second order linear ordinary diff. eq, so the solution must have two unknown constants, and it should be familiar enough that we can write down the solution by inspection. There are two possibilities:

1) If E is positive, (i.e. k is real) then

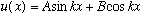
2) If E is negative, let 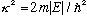, and then .

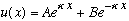Look at case 2 first - no matter what A and B are, this function can only have one zero. (Differentiate and set to 0, or just think about what the graph is like)

But we require u(x) to vanish twice, at 0 and a, so case 2 is impossible!

In case 1, when x=0, we get u(0) = B, but u(0)=0, so B must vanish.

Now look at x=a. There we have u(a) = A sin ka = 0. We could solve this by letting A=0, but then we'd have A=B=0, so u(x)=0, which is not only trivial, but it can't be normalized! So that's no good. We must keep A nonzero. The only possibility remaining is for k a = n pi, where n is any positive integer. (0 is no good, and negative integers are equivalent to changing the sign of A, which is still arbitrary, so they really aren't distinct solutions.) Putting this all together, we have found u(x), and also, because of this condition k a = n pi, we have found E as well, since 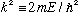. We label the solutions by this integer "n":

.

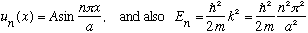The boundary conditions, u(0) and u(a), were what forced the energies to be quantized. The normalization condition fixes A:

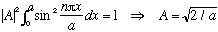
(I could always multiply A by any complex phase, that's totally arbitrary. In particular, the sign of A is ambiguous)

Some relevant notes and comments.

The first you might check from Boas Ch. 7, or Gas. 4-22:

1)

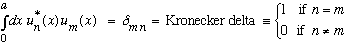
The "star" is not needed in this particular example since u is real, but it doesn't hurt anything. This equation says that "the u's are orthogonal, (orthonormal)"

The word "orthogonal" in reference to functions is reminiscent of orthogonal vectors (orthonormal => unit vectors), 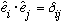, except we have an infinite number of unit vectors instead of only 3.

2) E_1 is not zero. The minimum energy has n=1 and is positive. (This arises from the Heisenberg Uncertainty Principle - since the particle is localized in a finite size box, it must have some finite, nonzero energy. If E=0, then it, and momentum, would be known exactly, a Heisenberg no-no.)

3) What is <p>?

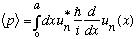. You can do the integral explicitly in this case (Boas does it), it involves a sin times a cos, with the same period, and this vanishes. You could also just notice that here, u(x) is real, so this integral is manifestly imaginary. But we already proved in Ch. 3 that <p> is always real, so if something is both real and imaginary, it must vanish. Bottom line,

<p> = 0, for any state n. (Does this make physical sense to you?)

4) What is <p^2>?

Again, you could just evaluate the integral explicitly,

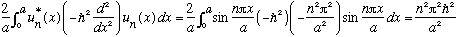
[NOTE TYPO - THE VERY FIRST "2/A" SHOULD NOT BE THERE, THOUGH IT DOES BELONG IN THE NEXT TERM. Sorry about that]

Or, you could notice that inside the box, V=0 => E = p^2/2m, so

p^2 = 2mE = constant, and thus <p^2> = 2m

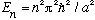
In general, the expectation value of kinetic energy in any wave function is

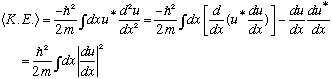
so you can see that the more "wiggles" u(x) has, the bigger the Kinetic Energy.

In our case, KE is everything, and as "n" gets bigger, the sin function wiggles faster (more nodes), and the energy grows like n^2.

5) The function looks like this:

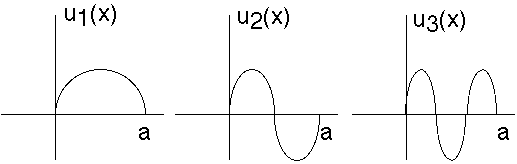
The solutions are either even or odd, with respect to the center of the well.

The number of nodes is always (one less than) the value of "n"

6) The set of functions, u_n(x), is a "complete set".

This is Fourier's theorem. What it means is that any function in the world, psi(x), which vanishes at x=0 and x=a, can be written uniquely ("expanded") as a linear combination of the u_n's,

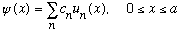
(For a proof of this, look at Boas Ch. 7) This last point is most significant!

Further discussion of this "expansion" idea:

If you want to find the c_n's, use Fourier's "trick", multiply both sides by u_m*, and integrate:

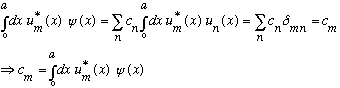
In keeping with our analogy between vectors and functions, i.e. , think of expanding any arbitrary vector in terms of a complete set of basis vectors:

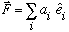
This can always be done, it is unique, and the a's can be found by the formula

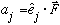, just like .

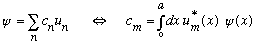(Integrating over x is the analogy of the dot product...)

The coefficients c_m in the expansion of 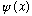have a physical interpretation! Intuitively, they tell you "how much of 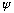is in the 'm'th eigenfunction".

(kind of like if you have a vector F = (F_1, F_2, F_3, ...), then F_i tells you how much of F is in the "i"th direction.)

Technically, it will really be 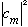that tells you the probability that psi was in the "m"th eigenfunction, as we'll see below.

In this example, the u_m's are eigenfunctions of H (the total energy) and so 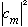tells the probability that the wave function 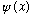has energy E_m.

Why is this? Next time, we will demonstrate it more explicitly.