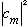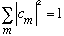Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 4, lecture 12 (9/22/96)

Here is the Next lecture

Back to the list of lectures

If we believe that 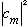is to represent a probability, then I expect .

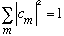It's not hard to prove that this is the case:

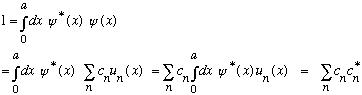
Also, if 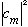is to represent a probability that we have energy E_m, then I would expect 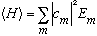. Again, it's not hard to prove that this is the case:

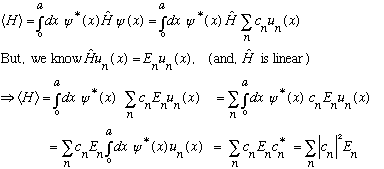
(These two conditions are basically all you need to demonstrate this probability interpretation is correct. )

Summary of this whole example of "expansion":

Any arbitrary state, 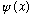can always be written ("expanded") as

,

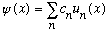where the u_n(x)'s are eigenfunctions of energy, and the c's are some set of coefficients (numbers). Since the u_n's each have a unique energy, but psi is a linear combination of different u_n's, psi does not have a unique, well defined, energy.

If you start in the state 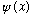, the number 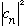equals the probability that a measurement of energy will yield the value .

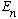Yet more notes and discussion regarding "expansion":

* In the example we've been studying, E_n is discrete. So, there is no range of energy involved, no "dE" anywhere, the probabilities are all just finite numbers.

* We already discovered that only certain, quantized, E_n's were possible. These are the only energies you will ever physically measure!

* The state 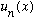is an eigenstate of energy, so it has a definite energy. If you measure energy in this state, you will always (repeatedly) get .

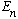* If you start with a more general function 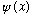which is not originally an eigenstate of energy, and then you measure the energy, you will always get some value 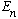(one of the eigenvalues) with probability 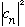. This "collapses" the wave function, because now you do know what the energy is. If you keep measuring the energy again and again, you will keep getting the same result, 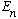. Measurement of energy can change your wave function - it started off as 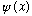, but measuring the energy put it into the state 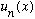. (You just can't know beforehand which value of n you'll get! That's what the 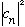tell you - which ones are more likely. )

* All the arguments and discussion above are extremely general! They will be true no matter what the potential is (not just a square box), and we will also be able to expand in a complete set of eigenfunctions of any operator, not just energy.

* If you are in the state 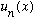, then

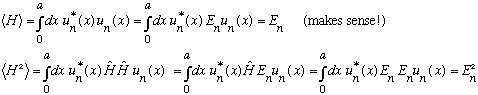
(NOTE THE TYPO: In the very first equation, I left out the "H" operator which should be sandwiched between the u^*_n and the u_n. The rest is all o.k.)

The formal definition of the uncertainty in energy is given by

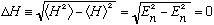
Which means there is no uncertainty at all in the energy. This makes sense - u_n is an eigenstate of energy; it has a definite value.

* Time evolution of any initial state is surprisingly easy. Suppose

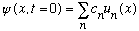
Go back to our original separation of variables, and you will see that the full, time dependent solution to the S.E. is just

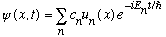
Each eigenfunction u_n gets the simple exponential time dependence, and superposition says you add up these products. The final result, of course, is a pretty complicated time dependence, but at least it's easy to write down.

Example:

Suppose you start in a state which is not itself an eigenfunction, but is a linear combination of the lowest two eigenfunctions.

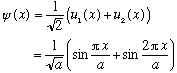
I can immediately write down the full time dependence, exactly:

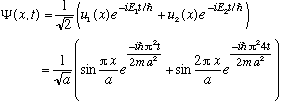
It's rather complicated looking. Let's check the normalization:

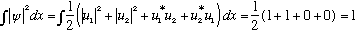
(The latter two terms vanish by orthogonality of wave functions. If you don't believe it, try integrating explicitly, u1 and u2 are simple sin functions.

The 1st two terms are already properly normalized.)

At a later time, t, we get

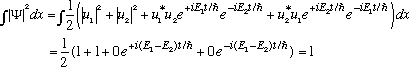
(Probability is conserved for all times, of course)

If I asked "what is <x>?" for either u_1(x) or u_2(x) by itself, you could argue by symmetry that it must be a/2. (Just plot them, or integrate explicitly, if you're not convinced that )

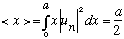But in this superposition example, with those cross terms in there, <x> depends on time!

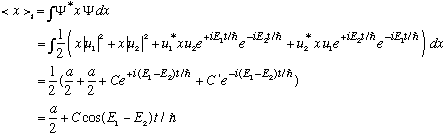
where 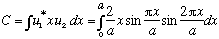is some calculable real number (times "a") (the number is a bit of a pain, I get something like -16/9 pi^2)...

It is enlightening to stare at plots of the wavefunction. I will show it at time t=0, and then again a short time later. Because the time dependence in the exponentials is different (u2 has a higher frequency), the relative phase of the two terms is always changing. Since u2 has a higher frequency, there is a time t1 such that u2 has gone through two cycles, and is thus exactly back where it started, but u1 has only gone through 1/2 cycle, so has flipped sign:

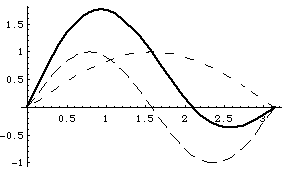
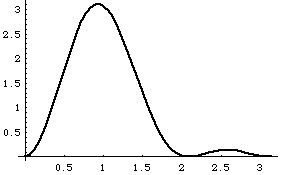
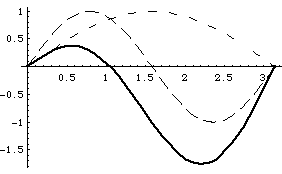
The top left curves show u1, u2 (each dashed) and Psi = (u1+u2) at time t=0.

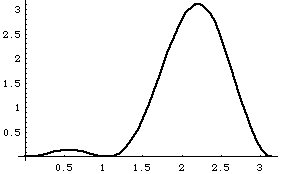
The top right curve is |u1+u2|^2, i.e. the probability distribution for |Psi|^2.

The lower left curve shows u1,u2 and (-u1+u2), (i.e, Psi at time t1)

The lower right curve is |(-u1+u2)|^2, i.e. probability distribution at time t1.

The wave function is apparently "sloshing" back and forth with time!

If you measure the energy of this system, you can only get one of two possible answers, eithe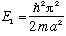r or 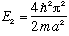. But, what is the average, or expected value of energy?

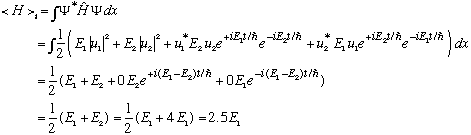
The average or expected energy is 2.5 E1, which is not an eigenvalue of energy!

It is also not time dependent, energy is conserved! And, you should note that this result can be found much more easily from our earlier formula:

.

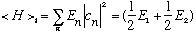We can also calculate <H^2>, and again I get the simple result

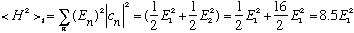
(I can get away with using this simple formula, because any eigenfunction of H is going to be an eigenfunction of H^2 too.)

Going back to my formal definition of uncertainty,

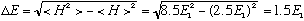
We got E = (2.5 +/- 1.5) E1. The two extremes of this formula give 1, and 4 (nice!), but most important, in this state, the energy is uncertain, and not well defined. A purely quantum idea!

(Next lecture will finish up some details of the above example, and start another "expansion" example)