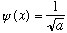Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 4, lecture 13 (9/24/96)

Here is the Next lecture

Back to the list of lectures

Again we have a particle in this usual box, and now suppose 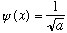everywhere inside the box (0 < x < a) and of course 0 outside.

This is a particle "uniformly spread out" inside our box.

What is the probability of measuring some particular energy E_n?

The answer, as usual, is 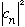, where .

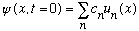We must simply figure out the c_n's. Fourier tells us the answer,

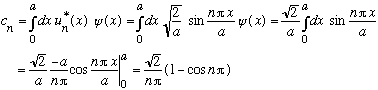
When n is even, this gives 0. (Symmetry tells us this! Even n's are the eigenfunctions that run through 0 at the center, and are antisymmetric about the center. But psi is symmetric about the center!)

When n is odd, this says the Probability is 8/(n^2 pi^2)

A little math check is in order here:

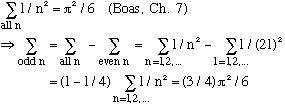
The sum of all our probabilities is (8/Pi^2) (3/4) (Pi^2/6) = 1 !! Nice.

Gasiorowicz (p.62) has a very similar, but algebraically harder, example. However, my example turns out to be a rather sick one, mathematically. That's because my psi does not go to 0 at the edges, at least, not smoothly. This is very unphysical. To build such a wave packet you would need lots of waves of arbitrarily high frequency, to make such a discontinuity. I can easily prove it:

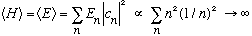
It would take an infinite amount of energy to build my wave packet!

Expanding in eigenfunctions of another operator:

Earlier, I looked at momentum, and found the eigenvalues and eigenvectors,

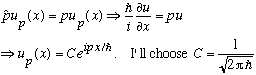
(The reason for the choice of normalization will come soon**).

The eigenvalues here are continuous, not discrete. You can have any value of p you want (unlike the energies in the box).

Before, we found that eigenfunctions satisfied an "orthonormality condition",

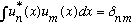, but now this equation doesn't really make sense, Kronecker delta's are only defined for integers. What we should expect is that in this case, with continuous eigenvalues, we'll just replace this equation with

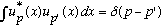(A Dirac delta function, rather than the Kronecker)

Similarly, we used to write our "expansion of an arbitrary wave function" as

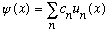
Again, since we have continuous eigenvalues, we expect the sum to become

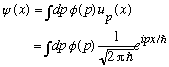
But hey, we know this phi! It's the Fourier transform of psi!

(**That's why I stuck in the funny normalization convention for u_p, so this formula would turn out to be exactly the same as the old Fourier integral, Gas. Eq 3-26)

We also know exactly how to invert this equation, and find phi:

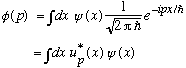
(The last line also fits into the same old pattern as before. Previously, with discrete eigenvectors, we would have written . )

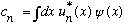We have already talked about how phi(p) is the "probability wave function",

i.e. 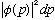= Probability of finding momentum in between (p, p+dp)

Again, this fits into the old pattern, where we have been saying

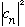= Probability of finding energy E_n.

Example:

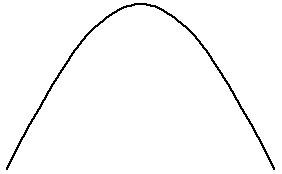
Consider the ground state of a particle in a box, that looks like this. If the box stays put, then only certain values of KE = p^2/2m are allowed, so it doesn't make sense to expand in momentum eigenstates (which would require all, i.e. continuous, values of p)

But suppose that, at t=0, the walls of the box were suddenly dropped

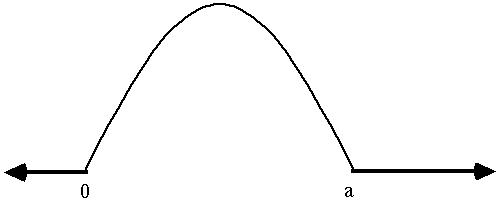
and at this point we allowed the wave function to evolve in time. (We know from Ch. 2 that the wave function will spread out) But, at this very first instant in time, if you measure momentum, what will you get?

The obvious guess might be 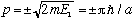. That, after all, is what we would have thought before opening the walls, and the wavefunction hasn't had time to change yet. But dropping the walls means that the potential is really time dependent, and classically that means energy is not conserved. So rather than guessing, let's just compute.

How do we find out what momentum we will measure? Find !

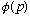Remember, 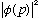tells you the probability of measuring momentum near p.

.

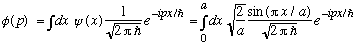To do this integral, rewrite the sin term using Euler's equation:

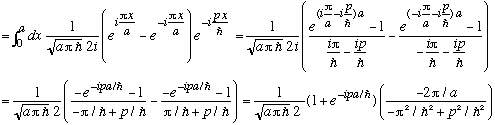
Yielding

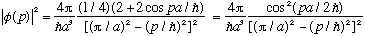
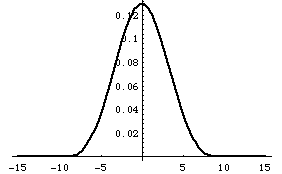
Here is the plot, versus "p a/hbar".

This function has a few wiggles you can hardly see, but basically dies away by about a couple Pi, i.e. by p=couple*Pi hbar/a

It's interesting, because I expected naively a particle in a box to have a momentum of about p= Pi hbar/a (plus or minus)

Here is the Next lecture