Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, Gas. Ch. 4, lecture 14 (9/26/96)

Here is the Next lecture

Back to the list of lectures

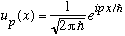These are also solutions to the Schrodinger Equation for a free particle, Hu = Eu, where H = p^2/2m. But there's something quite unpleasant about this wave function - it is not normalizable! If you try to find the norm, you get

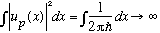
Why is this? If we have exact momentum, then the uncertainty principle says the uncertainty in x must be infinite - this particle is not localized at all. It must be "present" everywhere in the universe! And this can't be normalized, which seems slightly disastrous. We can still get away with making use of these "plane wave" wave functions, although you have to fix things up in some way.

Gasiorowicz discusses three strategies for getting around this business, each of which has its applications. (especially the third, which we will use again...)

1) Go ahead and use u_p(x), but understand that you should really use u_p(x)*envelope(x), where the envelope is a function that is roughly "1" over a huge region of space, but goes to zero somewhere far away from your lab. Then the integral will be finite, and you can normalize. This is called a "wave packet approach", where the wave packet is very nearly a plane wave, but not quite.

2) Imagine your "free particle" is trapped inside a huge box. This means that p is once again quantized, or discrete:

.

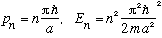Of course, "a" is huge, so the discrete values are very close together; the idea is maybe you won't notice they aren't continuous.

Also, the u's become .

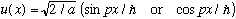(The amplitude is tiny, but again hopefully you won't care).

3) A practical approach is to think in terms of flux, because, after all, these "plane wave" solutions are supposed to represent a particle traveling along in the x direction with momentum "p". (=> a "current") We 1st defined flux in Ch. 3 (Notes 3-3 and 4). Recall the definition, and plug in the "plane wave" solution 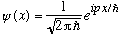to find the flux,

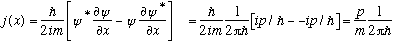
Classically, a spatial charge density rho(x) of particles traveling at speed v gives

flux = j = current density = rho*velocity = rho*(p/m)

Thus, it appears that our "plane wave"

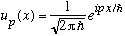
physically corresponds to a flow of particles, with a spatial density

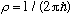particles/cm.

And of course, if 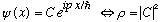particles/cm. (So, we can fix up the till-now arbitrary constant out front to reproduce the physical particle density)

(In 3-D, |C|^2 = particles/cm^3, by the way. )

Bottom line: If we ask physical questions assuming we have an infinite number of particles, but with uniform density |C|^2, moving with definite momentum p, then non-normalizability may be o.k. (It simply means that we have an infinite number of particles, not just one.)

Two final observations:

1) For free particles, in infinite space, as we've stated already,

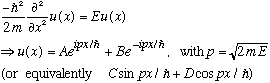
There are 2 independent wavefunctions here.

(Recall in a box we only got 1 wavefunction, because of the boundary condition.) These 2 independent wavefunctions have the exact same energy.

We say they are degenerate.

(There are 2 independent eigenfunctions with the same degenerate eigenvalue.)

These two solutions are still orthogonal (if k is not 0), by which I mean

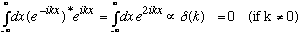
The two degenerate eigenfunctions can be distinguished by some other Hermitian operator. (This turns out to be a general feature of Q.M.)

In this case, the other operator is momentum: .

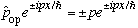Our 2 wavefunctions have the same energy, but different momenta.

2) I could look at these 2 independent u's as sin(p x/hbar) and cos(p x/hbar) if I wanted. These are still explicitly (degenerate) eigenfunctions of energy. But, they are not eigenfunctions of momentum anymore. (Check, if you don't believe me) So, what distinguishes this pair of degenerate, orthogonal, eigenfunctions?

There is another operator, in this case it is called parity, denoted by 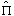, or P.

The definition of the parity operator is that 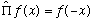. (Parity reflects about the origin)

What are the eigenfunctions of this operator? To find out, we must have

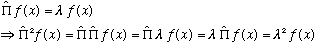
But P^2 is the same as doing nothing (flipping x about the origin twice takes you back where you started), so this last line must equal f(x) again. Which means

.

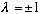That's the only possibility! There are only two eigenvalues possible for parity.

What are the eigenfunctions of parity? By inspection, any fn which is even, i.e.

,

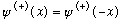is an eigenfunction of parity, with eigenvalue +1: .

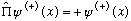Similarly, any odd function, i.e.

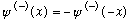
is an eigenfunction of parity, with eigenvalue -1: .

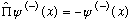Getting back to our starting question, we can now see that sin(p x/hbar) and cos(p x/hbar) are degenerate in E, but they are eigenfunctions of parity with different eigenvalues (one is -1, the other is +1). Parity distinguishes them.

Additional comments regarding parity:

* I suggested before that any arbitrary functi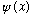on should be expandable in a complete set of eigenfunctions. (So far we've already expanded in eigenfunctions of energy in a box, and also in terms of eigenfunctions of momentum in free space) It's really a very general idea, you can always expand in eigenfunctions of anything, even parity. That is, any function can be expressed as some unique linear combination of an odd and an even function:

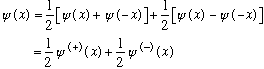
* If starts out even (and if it represents a wave fn in a box), then

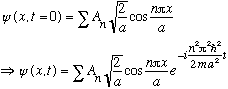
[NOTE typo: There's a factor of hbar wrong in the exponent]

it stays even forever! (Same for odd functions)

* If the box was not symmetric to start with, the previous statement would no longer be true, because the energy eigenfunctions would no longer be even/odd.

Symmetry in H <=> symmetry in the eigenfunctions !

A more mathematical wave of describing this is as follows:

If 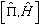=0, then the parity of wavefunctions will not change in time.

(More generally, if 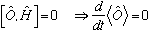) Why is this?

A symmetric box means V(x) = V(-x), which has the following consequence:

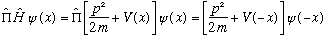
and also

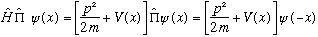
As long as V(x)=V(-x), these two expressions are identical, i.e.

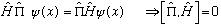
So we see why "symmetric box" is equivalent to .

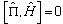But, why does this guarantee "conservation of parity"?

There are many possible proofs. Here's a rather direct one:

We know

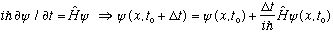
Now suppose that we start off in an even wave function at t0. Then

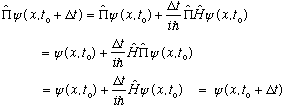
which shows that we are still even at a later time. (Proof is same if we start odd.)

Symmetry is incredibly useful and important in Quantum Mechanics. We have just seen the first example, where

a symmetry <=> a constant of motion, or a conservation law.

(and was mathematically connected with commutators)

As you know so well from Classical Mechanics, and E+M, conservation laws are handy, important, and often save a tremendous amount of work!

The opposite is true as well. If 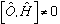, then in general <O> will not be a constant in time.

You can generalize even further: if [A,B] is not zero, then the set of eigenfunctions of A cannot be the same as the set of eigenfunctions of B. We say that the observables A and B are incompatible. (An example is x and p, which do not commute.) We will discuss this more, soon enough (Ch. 6).