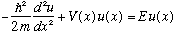
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 15 (Mon Sept 29, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Gas., Ch. 5

We will be working with the TISE (Time Independent Schrodinger Equation)

throughout this chapter, H u = E u, where E is some constant number:

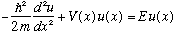
We will begin with some examples where E>0, i.e. the particle is not bound. Such a wave function, or state, is often called a scattering state, because the physics represents a particle traveling along, scattering off a potential, but not getting stuck.

Example 1: The potential step.

Suppose our particle comes in from the left (or, thinking back to our discussion of flux in Ch. 4, a steady stream of particles comes in. Or, also from that same discussion, we could send in some sort of wave packet:

In this case, you would need to Fourier transform, see what each component "k" does, and then resum at the end. )

This is kind of painful, although numerically it's not so awful, and is what's done in real practical cases. There are some nifty Java applets on the web that show this...

• 1) Simulate 1-D wave packets scattering off of barriers.

• 2) Another simulation of wave packets .

If there were no potential (V(x)=0) we would have free particles => momentum eigenstates => u(x) = .

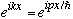But this example is a step function potential, ,

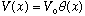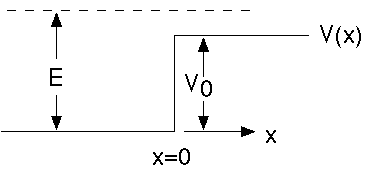
I assume our incoming particles have a definite energy, E > V0, which is given,

and we will slightly rewrite the TISE like this

:

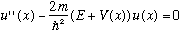It is convenient to define two new constants,

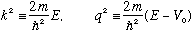
Both are real, positive, and known, given the sketch.

With all this, our TISE (writing separate equations for pos. and neg. x) is

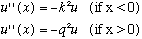
These are very easy differential equations, which I can solve by inspection:

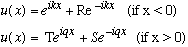
R, S, and T are unknown constants of integration. I could have put yet another constant in front of the very first term, but I chose it to be "1", since we're going to use the method of flux, which means we won't bother normalizing u(x)!

Also, S must be 0, because (again think of flux), the presence of such a term would be interpreted as particles moving to the left (from + infinity), and I stated that we only had particles entering from the left, traveling right!

We know that u(x) must be continuous everywhere (because the TISE has no infinities in it).

We also know that u'(x) must be continuous everywhere (same reason).

Thus, at x=0, we must have

1+R = T (continuity of u)

ik(1-R) = iq T (continuity of u')

Solving these two equations in the two unknowns R and T yields

R = (k-q)/(k+q)

T = 2k/(k+q)

(You should check this!)

Next time, we'll look at the resulting flux...

Here is the Next lecture