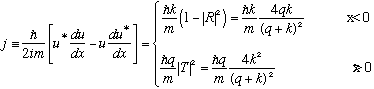
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 16 (Wed Oct 1, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

T = 2k/(k+q)

The flux is a little tricky to compute (we've done this for plane waves before), you will be checking this result in your homework this week:

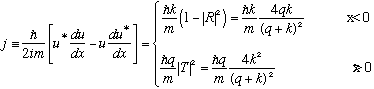
(I've plugged in the results for R and T in the far right expressions)

The flux is the same everywhere! Of course, this had to be the case, because it's a time independent problem, and 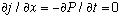=> (j=constant). (Probability can't "build up" anywhere in a time independent situation)

The fact that |R|^2 is not zero is rather neat. Particles are reflecting off the step! This is not a classical effect, since E>V0, classical particles would just "roll right up" the step, and keep going. For waves, though, it's not entirely unfamiliar - light hitting a piece of glass from one side behaves just like what we worked out here. Some reflects, some transmits...

If E >> V0, then the formulas show that k = q (roughly), and

R -> 0, T -> 1. (We do recover classical results for large energy.)

Example 1b: What happens if E < V0?

Nothing we did above is wrong in this case, but q is now imaginary, i.e. q = i|q|. The mathematics is the same, but now we find

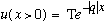
(This looks a bit like the dying EM field outside of a piece of glass, when there is total internal reflection going on)

Since u(x>0) is now real, there is zero flux for x>0. Also,

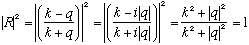
The net flux is zero everywhere, and there is 100% reflection, even though u(x>0) is not zero!

How can this be?

In the region x<0, there is a superposition of a plane wave traveling right, and a plane wave traveling left of equal amplitude. So the flux in this region is a sum of a positive (right hand) flux, and a negative (left hand( flux, which cancel, giving zero. The EM analogy is a wave reflecting off a boundary, setting up a "standing wave", which is really not traveling either left or right.

Example 1c: What if V0 is negative, but E is still positive?

This is now a step down potential. The math is essential identical to what I did first. You'll just plug in a negative number for V0, but the results from Ex. 1a still hold. This means you still get some reflection, even for a down step. This is very weird, and highly nonclassical. (Thelma and Louise might have "bounced" back from the edge of the canyon?...)

Example 2: The potential well

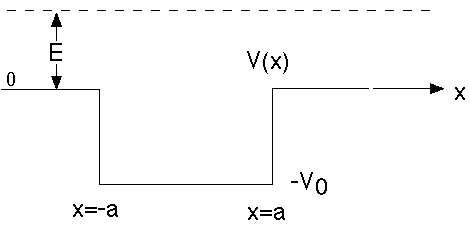
Once again, we send particles (electrons) in from the left side.

(Note the slightly different conventions in this graph from the previous example)

We make similar definitions as before (just flip the sign on V0 since it's dropping, rather than rising like it was in Ex. 1)

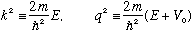
The S.E. is the exact same as in Ex. 1, and the solutions, by inspection, are

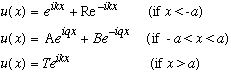
As before, we set one coefficient arbitrarily to 1, since we don't normalize,

and we only have a "T" term for x>a, because there's no flux entering from the right.

Continuity of u and u' at x=-a gives 2 equations. At x=+a gives another 2.

This means 4 equations in 4 unknowns (R, A, B, and T) They're a bit of a pain to solve: use the last 2 eqns (at x=+a) (sum and diff) to get A(T), B(T), then plug into the sum and diff of the 1st two eqns (at x=-a) to eliminate A, B, yielding finally

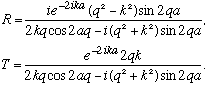
Not the most illuminating results in this form. (Of course, it's the absolute value squared that's most "physical", those are the reflection and transmission probabilities)

Note that when E>>V0 (k is very close to q) these formulas give |R|^2 -> 0,

|T|^2 ->1 (as you would expect). (It's slightly trickier to show the latter.)

Once again we get the nonclassical result that |R|^2 is not 0 in general!

Here is the Next lecture