Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 17 (Fri Oct 3, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

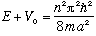
This is when the energy (above the bottom of the well) is exactly the energy for a particle trapped in an infinite box of width 2a. At this energy,

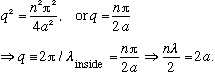
(The De Broglie wavelength "fits" perfectly in the well. Looking back at our formula for R, we see in this case sin(2qa) = sin(n pi) = 0, and |R|^2 = 0.

This is called a transmission resonance, there is no reflection for these special energies. (There is a crude optical analogy with "glare free glass".)

This phenomenon was observed by Ramsauer and Townsend, scattering low energy electrons off Ne or Ar. They saw certain magic energies, which fit the above formula (modified for 3-D) where suddenly there was very little scattering, and the beam just passed right on through the gas.

Example 3: Potential Barrier

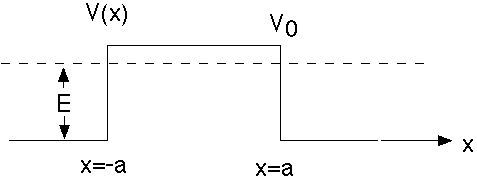
This example is just about identical to the last one, except V0 -> -V0. If E>V0, then it is almost exactly the same as the previous problem, and all mathematical results carry through almost without change.

If E<V0, as shown, there is a slight change. Now we define

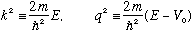
and note that in this case q is imaginary (like in Ex 1b.) We define

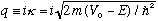
Just take the old formulas, replace q -> i kappa, and you're done! So, e.g, inside the barrier, the wave function now looks like

.

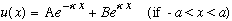The previous transmission coefficient formula now looks like

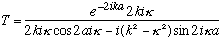
But cos(ix)=cosh(x), and sin(ix)=+isinh(x), so this gives

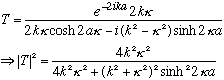
(I slipped in cosh^2-sinh^2=1 in the last step. Recall .

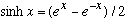Gasiorowicz made a sign mistake in the denominator of his Eq. 5-34.

The important thing is that |T|^2 is, in general, not zero! There is tunneling through the barrier. Once again, this is absolutely classically forbidden. The particle does not have enough energy to climb over the barrier, and yet somehow finds itself on the far side, at least, some small fraction of the time.

See Gas. for a discussion of what on earth we can make of a particle found inside the "forbidden" region, where E<V0, i.e. where it has negative kinetic energy! An E+M analogy might be light inside glass, hitting a boundary where it should totally internally reflected. If there is another piece of glass not too far away, some light can "leak" through the air barrier.

When ( 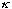a) is large (this could mean "a" is big - a wide barrier, or else

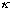is big => V0-E is big: a tall barrier), our formula simplifies:

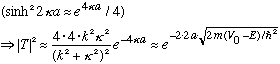
The very last approximation is crude, but the exponential is tiny, and the multiplicative factor out front ranges from 0 -> 4 (depending on the ratio of kappa to k running from 0 to infinity), so it's an order of magnitude approx.

The final form is suggestive of a more general result:

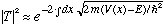
Gas. has a very crude derivation/justification of this formula. The real derivation is called the WKB approximation. The approximation involved is that V(x) must vary slowly in comparison with h/p. Griffiths, in Ch. 8, does it right! We won't go through the derivation, but will simply use the result.

There are a lot of important applications and consequences of this formula, including Scanning Tunneling Microscopes (STM's), superconductors, Josephson Junctions, emission microscopes, and many more! (Gas. pp 82-86)

A lovely example of the WKB approximation is decay of nuclei.

George Gamow first calculated this in 1928! It was a spectacular demonstration of the power of QM, and the phenomenon of tunneling, as well as a fine early model of the nucleus, all in one calculation.

Alpha particles are He nuclei, Z=2 objects (2 p's, 2 n's) which are bound inside atomic nuclei.

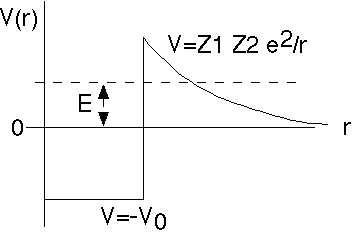
The nuclear binding potential looks something like this. -V0 represents the strong nuclear attraction. Z1 Z2 e^2/r represents the Coulomb (electric) repulsion once the alpha gets outside.

(Z1 = nuclear charge, Z2 = alpha charge = 2)

The energy, E, represents the energy of the alpha, both in the nucleus and after it escapes.

As you can see, the alpha is not really bound (since E>0). But, there is a huge potential barrier blocking it, holding it inside.

If, (at t=0), the alpha is inside, you can calculate the probability that it will tunnel out, when it "hits" the wall:

Prob =

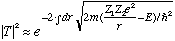
We need to know the limits of integration, which are the r values where the kinetic energy goes negative (the "forbidden" region).

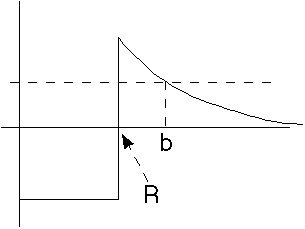
From this figure, the lower limit of integration is R, the nuclear size. This is about (1.5 fm) .

(You can find this independently, e.g. via

Rutherford, or electron, or gamma scattering.)

The upper limit of integration is "b", where

E=Z1 Z2 e^2/b.

The argument in the square root involves ,

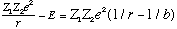and we need to perform the integral :

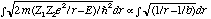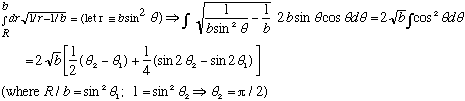
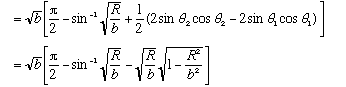
If b>>R, this is roughly 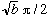, and

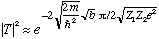
We could define a typical alpha velocity by

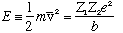
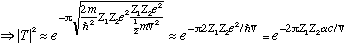
Our particle is "hitting" the wall once every t=2R/ seconds, i.e.

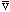/2R times/sec. So, the total probability of breaking through/sec must be

Prob = |T|^2 (prob/try) * ( 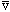/2R) (tries/sec).

The lifetime should then be roughly the inverse of this:

lifetime

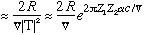
This "velocity" we defined is

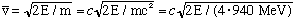
and finally

ln(lifetime)

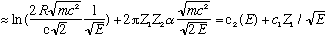
For E about 1 MeV (pretty typical alpha energy), I get c1 is about 4, and c2 is about -50 (for a big nucleus), which is in fantastic agreement with data. (See Gas. Fig 5-9)

Note: The probability drops extremely rapidly as Z1 increases, which is also why fusion (the inverse reaction) is far more likely for low Z nuclei.