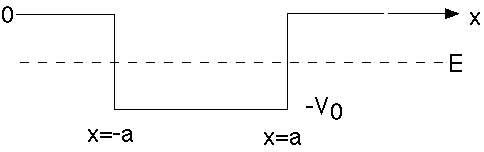
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 18 (Mon Oct 6, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

(Last time, we finished up our discussion of "scattering states", with the classic example of alpha particles tunneling out of a nucleus.)

The next topic will be bound states (E < 0)

The potentials will be some of the same one(s) we've already looked at, but now we're going to let the energy be negative, so the particle is trapped.

The first example is the "finite square well":

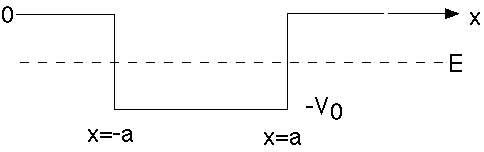
As usual, we make some definitions:

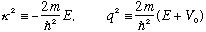
(Chosen with the sign of E and V0 in mind, so kappa and q are real)

Schrodingers Eq'n, again as usual, is =>

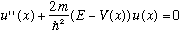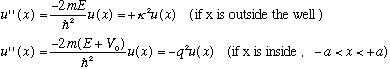
Again, by inspection, we can write down the solution for u(x).

Outside, it can only be exponentials,

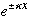
Inside, it can only be waves,

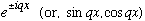
We can take advantage of our brief discussion of parity (from Ch. 4). Here, V(x) = V(-x) (by inspection), and this means (as we saw before), [H,P]=0.

=> the eigenfunctions of energy and the eigenfunctions of parity are the same! (Another way of saying this is that if V(x) is symmetric, then the energy eigenfunctions will either be even, or odd, but not some weird mixture.) We will consider the 2 possibilities separately:

1) Even eigenfunctions of H:

When x>a, the solution is a positive or negative exponential. But clearly for x>a, the positive exponential is bad - it blows up, and is not normalizable.

(Similarly, for x<-a, we cannot have a negative exponential, same reason.)

So, any even eigenfunction must have the following generic form:

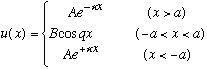
Symmetry has forced us to include only the cos(qx) term in the middle (because cos is even, sin is odd), and also "A" is the same for x>a and x<-a.

Continuity of u(x) at the point x=a says

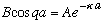
Continuity of u'(x) at the point x=a says .

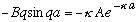Dividing the last two equations says .

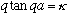Remember, the unknowns (q and kappa) depend only on E. Thus, this last equation really involves only 1 unknown, E, and fixes it!

If it fixes E, then it also fixes q and kappa! (However, as we will see, there are many solutions, which we will label E_n, as usual. )

Once we know E (and thus q and 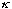) the 1st continuity equation tells us "B" in terms of "A". The 2nd continuity eqn adds no more information. Normalization fixes "B" (and thus "A"), and we know everything!

(If you look at x=-a, you will discover that neither continuity of u, nor of u', tells us anything new. That's because we've already made use of parity to write an explicitly even solution! Had we not been so clever, and left the solution totally general, there would have been two more constants (something like "C sin(qx)" in the middle, and D exp[+ 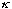x] for x<-a) and continuity at x=-a would have fixed "C" and "D" for us. But this is far more painful than what we just did!)

Here is the Next lecture