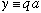 (This is a pure unitless number, check units!)
(This is a pure unitless number, check units!) Physics 3220, Fall '97. Steve Pollock.
Here is the previous lecture
Here is the Next lecture
Back to the list of lectures
Last time we set up the problem of a bound particle in a finite box. (Negative energy, even solutions) Today, we begin by focusing on the most interesting part of this problem - the eigenvalues of E:
First, define
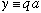 (This is a pure unitless number, check units!)
(This is a pure unitless number, check units!)
Next, let me also define another pure unitless number
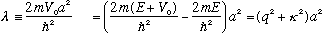
(We will find, repeatedly, that's it's easiest to solve math problems when they involve pure, unitless, numbers!)
So our eigenvalue equation,
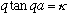 ,
becomes
,
becomes
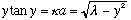 .
.
If I can just solve this equation for y, then I know q, and thus E, and I'm done! (Remember, lambda is known already, only E is unknown...)
This equation is "nonanalytic", there is no simple closed form expression for y
as a function of lambda. But, it certainly has solutions. They can be found
numerically, or graphically. Here's a graphical solution for
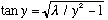 :
:
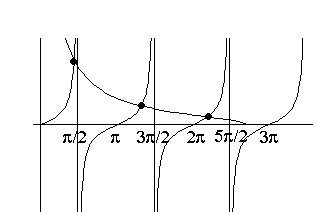
This is a plot of tan(y) vs y, and (superposed on top)
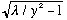 vs y.
vs y.
At the intersection points, (the heavy dots in the figure), the equation is satisfied. Just look down, and read off the values of "y". (And, knowing y => q => energy!)
You can see that there are a finite number of solutions (not infinite)
The
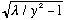 curve (the one that droops down) hits the y axis at
curve (the one that droops down) hits the y axis at
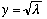 .
.
As lambda gets bigger (i.e. deeper and/or wider potential) that droopy curve rises and stretches, there are more and more solutions, and they tend to lie very near (slightly below) where
y = an odd integer number of half pi's. (i.e.
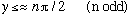
At these points,
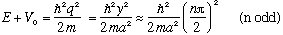
This formula makes sense, we've even seen it before: E+Vo is the energy above the bottom of the well, and this formula is exactly the same as the energies for the infinite well, for odd n (i.e. even wave functions) Of course, large lambda should agree with this, since large lambda should approach the infinite well. We're only getting the energies for the even functions, because we're only looking at even solutions so far!
When
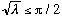 ,
the graph shows there is 1 and only 1 solution. No matter how small
,
the graph shows there is 1 and only 1 solution. No matter how small
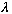 is, there is always a solution. (A very narrow and/or shallow well can
always trap a particle, but only in one very low energy state.)
is, there is always a solution. (A very narrow and/or shallow well can
always trap a particle, but only in one very low energy state.)
1) Odd eigenfunctions of H:
The game is basically the same, we make use of symmetry, and write down the general result for an odd function that solves S.E. in this well:
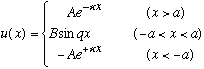
Just as before, but now use sin(qx), to make it odd. (note the -A for x<-a.)
Again, continuity of u and u' at x=a gets us an equation, which this time is
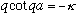 (check this!)
(check this!)
and, using the same definitions as before, this is equivalent to
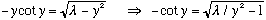
This time, the graph looks like this:
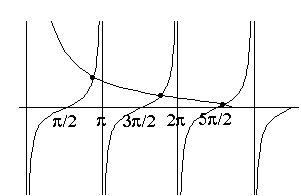
The plot is similar to the last one, in fact,
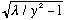 is the exact same, and -cot(y) is just like tan(y), only shifted by Pi/2.
is the exact same, and -cot(y) is just like tan(y), only shifted by Pi/2.
If you compare the two graphs, you'll notice these solutions (the black dots) come in between the even solutions.
There are thus equal numbers of even and odd solutions (give or take one), since they just alternate.
As lambda gets big, the solutions (just look at the picture) are now at
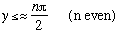 .
.
So we've picked up all the rest of the infinite well solutions (the odd wavefunction ones), which is good!
If lambda is really small (
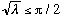 ),
there are no odd solutions (but there is still always the single lowest
even one.)
),
there are no odd solutions (but there is still always the single lowest
even one.)
The odd wave functions vanish at x=0. (by definition, since they must be continuous.)
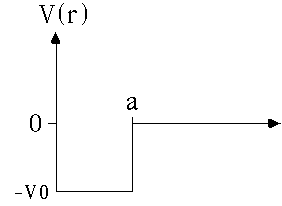
It's interesting and useful to note that the potential sketched here
(infinite at the origin, otherwise the same as what we've been looking at. It's sort of "half" of what we just looked at)
would give exactly the same solutions as what we just got for the odd u(x)'s.
They would have to vanish at the origin (here because the potential is blowing up) but elsewhere for x>0, this potential is identical to the one I've just looked at, so the solutions (and energies) must be the same. But this potential only matches the odd wave functions, because of the requirement that u(0)=0.
In the 3-D world, it will turn out that potentials always look like this (as functions of r) so when we get to the 3-D "finite well" problem, we'll already have done all the work...
New topic: delta function potentials,
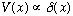
Example 1: a delta function in the negative direction (a narrow deep well)
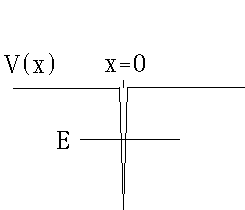
V(x) =
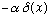 ,
,
and we're looking for a state(s?) with negative energy, i.e. a bound state.
Note that alpha above has units of energy*distance, do you see why?
(This example should agree with our previous case, in the limit that a -> 0,
and
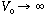 ,
as long as the area,
,
as long as the area,
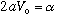 .
You could check this in the end.)
.
You could check this in the end.)
We are solving Schrodinger's Eqn, which looks like
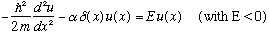 .
.
For all x away from zero, the delta function term disappears, and so the solutions are as usual,

For x>0, it should be clear we can only have the negative sign up in the exponential (otherwise u(x) will blow up at infinity). So, u(x>0) is a simple dropping exponential. Similarly, u(x<0) is a simple, pure, rising exponential.
Symmetry says the solutions must be even or odd. But odd doesn't make any sense here, because u(x) has to be continuous. (Think about this and convince yourself you cannot draw a continuous, odd graph with pure simple exponentials on both sides!) So our solution must look like
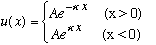
It's even (by putting the same A in both expressions), and automatically
satisfies the "continuity of u" at x=0, by inspection. Once we figure out
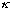 ,
if we normalize it, this will fix "A", and we'll be done. But, how to find
,
if we normalize it, this will fix "A", and we'll be done. But, how to find
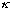 ?
?
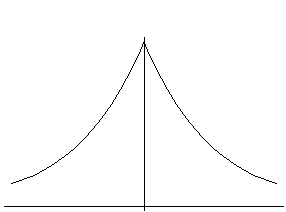
Here's a little sketch of u(x).
In the previous example(s), we invoked continuity of u'(x). We can't do that here! At x=0, u'(x) is not continuous.
Of course, that means that u''(x) will be infinite, but that's o.k. - there's a delta function in the equation at x=0, so we expect u''(x) needs to be infinite there!
So, we invoke a little trick. Write down the S.E., and then integrate it just around the origin, over a tiny region of x:
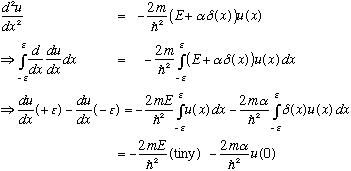
(Convince yourself that that integral of u(x) dx vanishes, if epsilon -> 0)
Next time, we will make use of this to finish the problem, and solve for the energy...
Here is the Next lecture
| 3220 main page | Prof. Pollock's page. | Physics Dep't | Send comments |