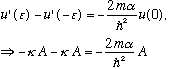
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 20 (Fri Oct 10, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Last time we set up the delta function potential problem (bound state). We integrated Schrodingers equation, so we have learned what the sudden change in the slope of u(x=0) is:

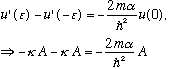
or in other words 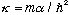. There is one solution, so there is only one possible bound state. This equation is independent of A, which is good. (As I said above, you now find A by normalizing.)

This equation implies

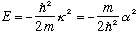
No matter how "strong" the well is (no matter how big alpha is), there is still only one solution.

Such a delta function potential may seem awfully mathematical to you, but it's reasonably realistic, at least as an approximation, for many potentials in nature. (E.g. for a quick and dirty estimate, a nucleus provides a well for electrons which can be modeled/approximated as a delta function with some appropriate strength.)

Example 2: What about if E>0?

This means we have a free particle, with positive energy, running past a delta function. Remember the beginning of this chapter - positive energies are "scattering" problems. We can't normalize the wave functions, but we can ask what the reflection/transmission probabilities are. Let's now define 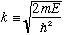(note the sign convention), and as always, by inspection, the solution of the S.E., 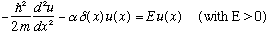, is

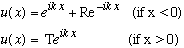
Continuity of u(x) at x=0 says 1+R = T. As in the last example, our potential blows up at x=0, so we cannot assume that u'(x) is continuous, but we can integrate the S.E. around the origin, same as above, to find

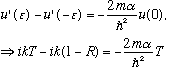
Let me define a new unitless (energy related) quantity, .

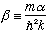Everything in that definition is a fixed, given constant. (In scattering problems, we're not solving for E because it's given, you should think of some beam of electrons being shot in from negative infinity, and we just want to know how many go on, and how many bounce back. Beta is directly a function of the beam energy, and also the potential well depth.

(Note also that beta is unitless, can you convince yourself of this?)

Our last main equation says

ik (T-1+R) = -2k T beta,

or (dividing through by k,)

i (T-1+R) = -2 T beta.

(We already had 1+R = T.)

This is two equations in only two unknowns (R and T), and they yield

i (T-1+ T-1) = -2 T beta => 2i(T-1) = -2T beta => T(i + beta) = i

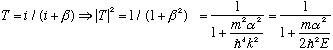
For large E, |T| -> 1, you go flying right past this little blip of a well and ignore it.

But, for very small E, |T| -> 0, and you bounce off the well!!

Example 3: a positive (upward) delta function potential

If you change the sign of V(x), i.e. let alpha change sign, this formula does not change!! So, you can run right through an infinitely tall barrier as though it wasn't there, if you have enough energy. (It's infinitely tall, but admittedly awfully narrow!)

Next example: a double delta function potential.

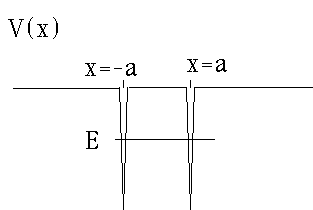
Such a double well is again more physically reasonable than you might think. It makes an excellent 1st approximation to a diatomic molecule, like H2. (This sketch might be the potential felt by an electron in an H2+ molecule.)

(You could think of it as the limit of two side-by-side square wells, each of which gets narrow and deep, but staying a fixed distance apart, like the potential due to the two nuclei in the H2 molecule.)

We write this potential mathematically as V(x)= .

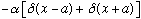As before, everywhere (except at x=+/-a), we have a free particle S.E, and

Also, our well is still perfectly symmetric, V(x) = V(-x). So, we know our solutions are going to be purely even, or purely odd.

Even solutions:

Recalling that the even combination of exponentials is the cosh, we get

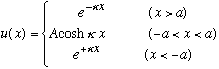
(I have left out a normalization constant. That's o.k. - at the end of the day, we'll just normalize u(x) with some overall multiplicative factor.)

Continuity of u(x) at x=a says

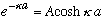
We can't use continuity of u'(x=a), because of the fn, but our trick says

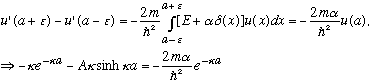
(NOTE the typo in the above equation. The argument of the delta function is (x-a), not x, of course) Plugging in 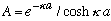gives

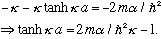
"a" is known, as is alpha, so this is purely an equation in one variable, kappa, which in turn is directly a function of energy. (This equation tells us the bound state energy.)

Next time, we will "solve" this equation graphically.

Here is the Next lecture