Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 21 (Mon Oct 13, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

I will play the by now usual game, defining unitless quantities

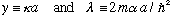
(Gasiorowicz in fact uses this 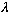right from the very start, rather than alpha)

We are trying to solve

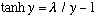
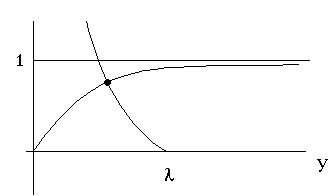
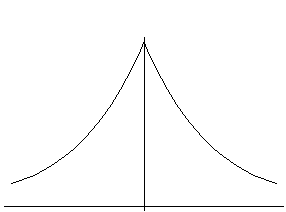
Here I show the plot of tanh(y) vs y

(it's approaching the asymptote of "1", which I drew in), and also

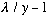vs y. (The dropping curve.)

There is apparently one, and only one, solution, no matter what lambda is.

Since tanhy = 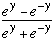<1, then 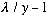=tanhy <1, and .

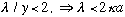This means kappa is bigger than 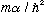, which was the result for the bound state energy for the single delta function well. The double well binds the particle more tightly.

(Also, by inspection of the graph, we must have y< 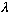, which results in kappa being smaller than 2 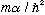. So we are not bound by twice as much as a single well!)

Before, we had : and now we get

In the single well, the discontinuity of the slope was fixed by alpha. In the double well, the same discontinuity in the slope means we get a steeper falloff outside of the "wells", and that means we're more tightly bound.

If 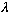gets really big, we expect our solution to go to 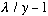=tanh(y)=-> 1

i.e. y is less than, but close to, 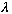/2, which was the single well energy.

Physically, the H2(-) molecule has a nice deep binding, even lower energy than an H and an H(+) would have if they were very apart. This, even though H2(-) has the additional Coulomb repulsion of the protons we haven't even taken into account! It's because the wave function is so much more "relaxed".

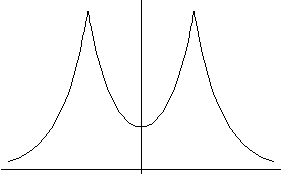
Odd solutions

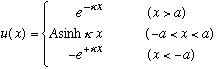
The same calculation as before now gives (check this!)

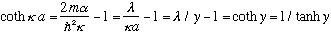
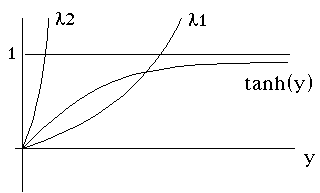
I've drawn tanh(y), and then two different curves of 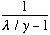, for two different values of lambda.

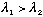
You might get a solution, if lambda is big enough, or you might not!

What is the condition which determines whether there is a solution or not?

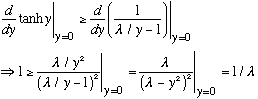
If 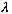>1, we do intersect (once), and get a single odd solution (+ the even one).

If 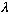<1, we do not intersect, there is no odd solution (only the even one).

The solution point lies to the left of the spot where

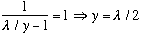
(because tanh(y)<1 everywhere), and this means 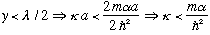which was the single well result.

If the double well is strong enough, there may be a second solution, but it will always be less deeply bound than a single well of the same strength. The reason can be seen graphically; our odd solution will look like this:

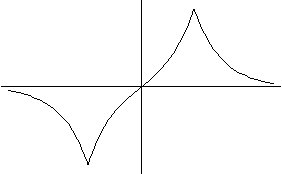
The curve is steeper in the middle region (to reach zero!) which means it will be less steep outside (because the change in slope is given by the strength of the delta function), and so it is less bound.

Example: Suppose an electron starts off trapped in such a well, but initially is located in the right side of the well. What happens as time goes on?

Since the electron is trapped, we know that the initial wave function must be a superposition of the two bound states, u_e(x) (the lowest, even one, and u_o(x) (the next, odd one). (It cannot be in a pure energy state, because these are both symmetric with respect to the center.) This means the normalized starting wave function can be written

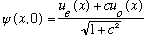
We want to choose c so that the particle is located mostly on the RHS. The most natural definition I can think of would be to pick "c" so that

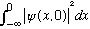is minimized. (This is a nice exercise, I won't do it here.)

But whatever c turns out to be, we can still study the time dependence:

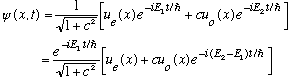
When 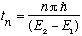(with n an odd integer), we will have the right hand exponential yielding -1, and so

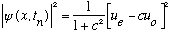, instead of

.

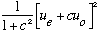By flipping the sign of the odd wave function admixture, we also flip the

side of the well we're located on; if it started off at t=0 localized on the RHS, at t_n it will be localized on the LHS, and this will oscillate smoothly in time, back and forth. The electron oscillates spatially with a frequency of

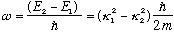
In a certain sense, you can think of this as another example of tunneling. The electron is initially "trapped" inside one of the wells, the right one. There is another well off to its left, but it doesn't have enough energy to climb up and over and go into the other well. But it can tunnel across to it, and it does so! (If you go back to our tunneling formulas, and make an estimate for the time it would take a particle to tunnel through the intervening barrier between the wells, you would find that this time is approximately the period of oscillation we just figured out.)

This is a crude, but reasonable, model for many atomic and molecular systems. E.g. in ammonia molecules, NH4, the 4 H's make a plane, and the N is then either on the left, or on the right. The potential is symmetric, but there are (just like in this problem) two bound states, one slightly deeper bound than the other, one is even, the other is odd. The energy difference between the two states is very low, so because of random thermal excitations, a bound molecule is generally not in the ground state, but in a linear combination of the two states, and so it oscillates back and forth as we just worked out.

(One can make a clock out of such an object, or anything that vibrates with a well known constant frequency...)

The Harmonic Oscillator: (sort of)

A harmonic osc. has potential energy

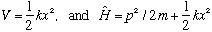
This problem is of such importance because any system with any force, as long as the displacement is small, tends to look like a harmonic oscillator:

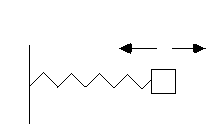
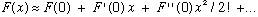
Near an equilibrium point, F(0)=0, we have .

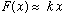Schrodinger's equation for the quantum version of this problem is

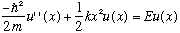
We make some definitions, to get unitless and/or more convenient variables:

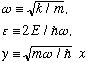
This def. of omega is fairly obvious, it's the classical frequency.

Epsilon is reasonable, especially since both the Bohr method and the uncertainty method (homework problems from Ch's 1 and 2!) gave us 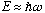, so epsilon looks like a "unitless" energy with a natural scale.

But where did this definition of "y" come from? A classical harmonic oscillator will have a maximum stretch of E= 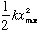, so if you assume ,

,

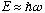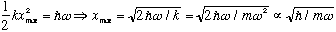so our y is proportional to x/xmax, a "unitless" position with a natural scale.

Now we want to change variables in our S.E. (It's always a wise thing to deal with differential equations that involve nothing but pure unitless variables.)

Don't forget to use 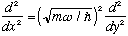, and you should find

.

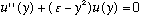Later this semester, we will solve this problem in a far more elegant way, but for now, let's use Gas' "brute force" way. One can almost always solve a differential equation like this by the method of power series (assume a power series form for u(y), plug it in, and get some recursion relations for the coefficients in your series).

But, it really helps if you can understand your differential equation first, and perhaps pull out some important asymptotic behavior. I'm going to skip some of the details (see Gas, pp. 104-108 for more information) We'll do this next time...

Here is the Next lecture