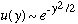Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 22 (Wed Oct 15, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

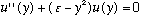If y -> infinity, the solutions behave, roughly, as 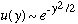. (This is not exactly correct, and you should see Gas' discussion, 5-127 to 5-131 if you'd like to understand it better) But, in any case, I can just use this, and try the following possibility (this is a definition of a new function h(y)):

.

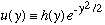(If the asymptotic behavior of u(y) really does look like that exponential, then the hope is that h(y) will somehow come out to be simple. If my choice of asymptotic behavior has been poor, or even wrong, then h(y) would just not be any simpler than u(y) was in the first place!)

Take this definition of u(y), plug it back into our differential equation, and we will get a new (equivalent) equation for h(y): (check this!)

.

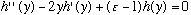Now, we will use the method of power series. (We could have done this for u(y) at the start, and it would even work, but the answer would not have been easy to understand, since of course that nasty exponential behavior would've been absorbed into the solution.) So, we try

,

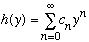and plug this right back in the differential equation. I get (check this!)

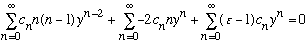
The first 2 terms in the leftmost expression vanish, and after that I can redefine the dummy sum index m = n-2, making that first term become

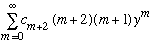
The conclusion (since each term in the power series must vanish!) is

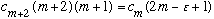
When m gets large, this says c_(m+2)/c_m goes like 1/m, which is bad!

(Look back at Boas, or any book on series. Such a series diverges!!)

But we can't have a divergent series; the only resolution is that our series must not go on forever! It must stop at some m_MAX. The only way to ensure this is for 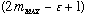to vanish!

(then, the formula above says the next c will vanish, and all other ones after that. The series ends at m_MAX, which I will call N from now on.)

We have

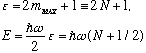
This last formula is familiar! Planck said that radiation in a box has energy which comes in integer chunks of 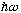. Apparently, the modes of EM radiation are closely related to harmonic oscillations.

We have now concluded that h(y) is a finite polynomial, of order N. These polynomials are called Hermite polynomials, .

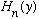The recursion relation above, ,

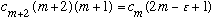tells us explicitly what the Hermite polynomials are (aside from an arbitrary overall multiplicative constant.)

Hermite chose a particular normalization,

.

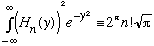Here are some explicit examples:

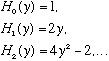
Gas. (P. 107) has various "factoids" about these polynomials (and we also saw much of this in 2140 - see Boas.)

They alternate even, odd, as we have come to expect.

Putting them back in to u(x), we find they are orthogonal, i.e.

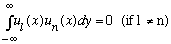
(The proof is rather interesting, see Gas,l end of Ch. 5.)

(If you need/want it, we can plug back all our definitions, to write down the complete wave functions u(x), but we usually won't need this)

Gas. Ch.6 : Basic Principles of Quantum Mechanics

The first part of Ch. 6 is in many ways a review of what we've been talking about in Ch.'s 4 and 5, just stated a little formally, introducing some new notation and a few new twists. We will keep coming come back to it -

be sure to read Gas. pp 114-118 for now.

I'm going to supplement Gas' treatment a bit here, you should look at Griffiths, Ch. 3, if any of the linear algebra is unfamiliar.

(Liboff, Ch. 3 and 4 are useful and relevant here, too)

First, a quick review of vectors:

* Vectors live in N-dimensional space.

* We have (or can choose) basis vectors: 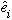(N of them in N-dim space.)

* They are orthonormal: 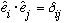(scalar, or inner, or dot product.)

* They are complete: This means any vector 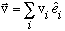is a unique linear combo of basis vectors.

* The basis set spans ordinary space. (Not so important for us, this is like completeness, but backwards - every linear combo of basis vectors is again an N-Dim vector, and all such linear combos generate all possible vectors in the space)

* We can choose a specific representation of v, namely 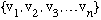, but it is not unique, it depends on the choice of basis. (e.g. polar vs. rectangular, and even which particular rotation of the rectangular axes.)

* Each number 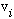is the projection of v in the 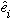direction, and can be obtained by the formula .

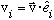(This involves the same scalar product, again, as we used above in the statement of orthonormality.)

You can prove the last formula by using orthogonality and completeness.

* Addition, or multiplication by a scalar (number), keeps you in the same N-dim "vector space". (adding or scaling vectors gives another vector.)

As I hinted at back in Ch. 4, we can make very powerful analogies to all of the above in the world of square integrable functions: Note the one to one correspondence between each of the following statements about functions, with the preceding ones about vectors.

* Square integrable functions live in Hilbert space. (Never mind what this means for now!)

* We have (or can choose) basis functions: 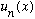(Infinitely many of them.)

(This infinity might be countable (discrete), or it might be uncountable, in which case you can't use integers as labels, but need real numbers.)

We have already met some examples of both such types of u_n's, as eigenfunctions of operators, in Ch. 4.

* They are orthonormal: 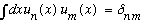. This is apparently our new way of writing the inner product. (If the labeling is continuous, the right side will be a Dirac delta function.)

* They are complete: Any function 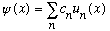is a unique linear combo of the basis vectors. (If the labeling is continuous, then 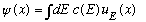) See notes, page 4-5.

* The basis spans Hilbert space. (Again, this one is not so important to us, and is similar to completeness, but backwards - any linear combo of basis functions is itself another square integrable function, and all such linear combos generate all possible functions in the space )

* We can choose a specific representation of 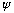, e.g. 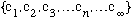if the labeling is discrete. (Otherwise, we need a function, like e.g. 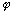(p))

But, it is not unique, it depends on the choice of basis. (More on this soon)

* The number 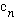is the projection of 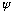in the 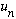direction, and

.

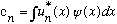(This involves the same scalar product, again, as we used above in the statement of orthonormality)

You can prove the last formula by using orthogonality and completeness.

* Addition, or multiplication by a scalar (number), keeps you in the same Hilbert space. (adding or scaling functions gives another function.)

The analogies don't even end here!

* Operators transform vectors (functions):

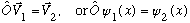
* Linear operators are defined by:

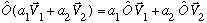
* Linear independence says: A is linearly independent of a set 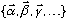if 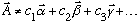for any set of constants, c_1, c_2, c_3,...

(Same for functions)

E.g, 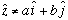for any "a" or "b", or e.g. 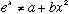for any "a" or "b".

This analogy is powerful, because it allows us to think of wave functions more abstractly, and to make use of lots of math we know and understand regarding vectors. 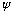(x) is, after all, just a collection of numbers, in the same way that v=(v_x, v_y, v_z) is a collection of numbers. Think how often in physics it is better to work with the symbol, or concept, of v: independent of any particular representation, or basis choice. (Choosing polar or rectangular or rotated coordinates will change the numbers v_x, v_y, v_z, but it will not change the vector, v!)

We will often use the notation 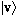, instead of v, for the abstract vector.

Similarly, we will work with the abstract wave function, and call it .

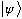We sometimes call this a "ket". This is our first example of Dirac Notation.

Here is the Next lecture