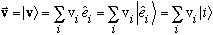
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 23 (Fri Oct 17, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

More Dirac Notation:

We may choose to write any abstract vector in terms of its components in some particular basis:

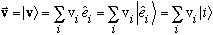
The first summation notation is the normal old one, the second is where I begin to think of my basis vectors as themselves abstract vectors (!!), and the third is just an obvious briefer notation (a shorthand notation for the basis vectors.)

The components of any vector, you will recall, are found by

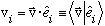
(This last is just a definition for an alternative notation for the dot product.)

In complete analogy, we will write

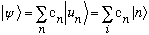
(The final notation is again just an obvious briefer notation, |n> is just a shorthand notation for the basis function |u_n>.)

Again, I am thinking of my basis states as themselves being abstract kets!

Any function, even basis functions, can be thought of as a ket, just like any vector, even basis vectors, are themselves just vectors.

The "ket" 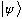somehow represents the state of a particle. But it doesn't have to be given in any particular representation, it's more general, more abstract. It's analogous to talking about some vector v - I don't have to tell you its components, I might describe it in some more general way, [perhaps it solves some particular equation....] If I need the components, I can pick some convenient coordinate system (rectangular, or polar, or whatever) and then figure them out.

E.g., we have already learned that 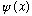and 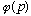(the Fourier transform) refer to the exact same particle in the exact same state. They are fully equivalent, carry identical and complete information about the quantum state. It's just that one is specifically in position space, the other is in momentum space. They will turn out to be two different representations of the one and only true abstract state .

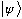It is a little unfortunate that (Gas, and I, and most books) use the same Greek letter "psi" for the name of the space wave function and also for the name of the abstract state. There's nothing special about the space wave function, it is really no better than 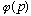. We just had to pick some name for the abstract state, and 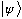seemed better than . (Using kets has the same potential for simplifying our life as does using vectors without specifying a coordinate system ahead of time.)

More Dirac Notation:

As we have already said, any state can be expanded in basis states:

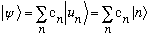
We have also seen the formula for the coefficients in this expansion:

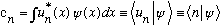
This is our scalar product for functions, and as I've mentioned earlier, we often use the "bracket" notation instead of the integral. It's a definition, the bracket notation is a shorthand for the integral. (The final expression is just a lazy shorthand for the first, when I get tired of writing u_n, and just label it by "n" alone)

By the way, the right half of a "bracket" symbol looks like thi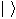s, , that's why we called it a "ket". And, I kid you not, the name for the left half, which we write like this, 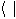is called a "bra".

There is already lots to observe about our new Dirac notation:

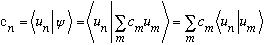
(The first is just the usual old formula, c_n is the inner product of Psi with u_n. The next statement is just obtained by expanding Psi as a linear combo of basis vectors. The final statement is just an observation that the summation comes out of the inner product [linearity!])

But 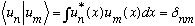: our statement of orthonormality.

What we had a few lines above now looks like

,

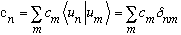which is manifestly correct.

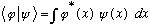is in general a complex, constant number. (And, don't forget the star on the "bra"'d function when you do the integral!)

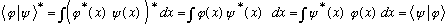
Starring a bracket just flips the two entries. You do not, in general, get back what you started with (unless it was real to begin with.)

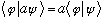(constants, even complex ones, slide right out of kets.)

But, 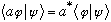(note the complex conjugate!)

I keep writing 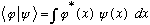, but I should stop, because that is representation dependent! It's like writing 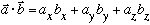. The equation is correct, but it depends on my specific choice of Cartesian coordinates. (in polar coordinates, the formula for the dot product looks different, but it's still the same result.)

For instance, it is equally true that 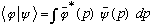, where the tilde on top means "Fourier transform of"... (We'll prove this later.)

You should try to think of 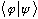as an abstract dot product. (If that's hard, its not wrong to think of it as that specific integral, it's just a little limiting.)

The "bra", 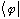is a slightly odder beast than the "ket", 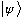. The latter is just like a vector. But the former is not a vector. In fact, it's more like an operator, except its not that either, because operators operate on vectors to give back another vector, while bra's act on vectors to give back a scalar (a number).

It's more like a function of vectors. I usually think of it like this:

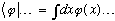
and you generally fill in the blanks with some ket.

(It's formally called a dual, if you really want to know!)

In the world of ordinary (complex) 3-D vectors, where

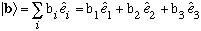(where the b's might be complex), you might be used to many equivalent notations, e.g.

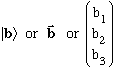
In this world, the notation for the dual would be

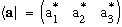
With this notation, the dot product is very simple:

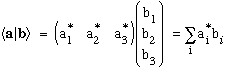
You're not used to those stars, but then, you're probably not used to complex vectors! The reason we put them there is so that the norm of any vector, namely the dot product of the vector with itself, is positive:

.

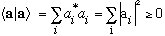The norm is technically the square root of this:

Norm(a) = Length(a) ,

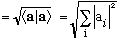For ordinary vectors you're used to, the star is irrelevant, and you just get the usual dot product and the usual norm.

A rather abstract and formal looking relation (but very useful), can now be introduced. First, think in ordinary vector space, and consider a projection operator, , which operates on a vector, and returns the projection of the vector in the n direction (which is again a vector.)

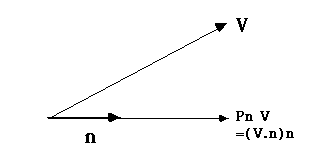
I claim that I can write the projection operator as

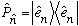
Why should this be?

Well, just operate P on a vector, and see what happens:

,

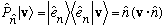which is precisely what the projection operator is supposed to do!

It returns a vector in the n direction, with length =

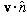
In Hilbert space, this projection operator is written 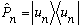, it projects into the "u_n" direction. This means

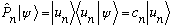
Projecting in the "n direction" gives back a "vector in the n direction" (here, the ket u_n) with a magnitude c_n.

Now, I would claim that

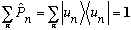
(That 1 is the unit operator, since projections are themselves operators.)

This mathematical statement is formally called "completeness", it says that if you add up projections in all possible directions, you always get back what you started with. (It's rather abstract, and admittedly a bit hard to understand at first!) Here's a rough proof:

Take any vector

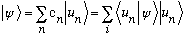
The above familiar looking statement is equivalent to

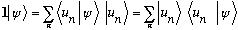
(The bracket of 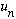with psi is just a number; it can be freely moved around)

But since this relation is true for any psi, we have an operator identity:

.

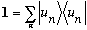You might want to check with ordinary vectors, to see how the identity looks:

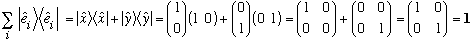
Note that putting the bra and ket in the other order gives

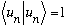, a number not an operator. (It's a totally different beast!)

Here is the Next lecture