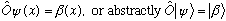
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 24 (Mon Oct 20, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Suppose we have an operator O that does something like this:

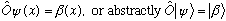
Then, we will define a new ket, which we call .

This is simply the name, or label, of a new ket. It is defined by

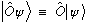
We thus have

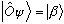
These are just two different labels for the same ket, so naturally

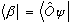
Putting these together with any other bra, 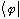gives

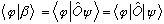
(The last two expressions are interchangeable notation, the 2nd vertical bar is basically there to guide the eye.)

This all looks awfully abstract, but we know what it means:

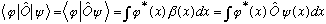
For reasons we'll see later, this expression is usually referred to as a

matrix element of O.

In the expression the operator O operates on psi (i.e. to its right) as usual. It does not operate on phi, which is to its left. However, I can define a new operator, related to O but possibly quite different, cleverly designed so that if it operates on phi, we somehow get back the same number as when O operates on psi. (Remember, the matrix element we're looking at is just some complex number.) This new operator is called the adjoint of O, or the Hermitian adjoint, or sometimes the Hermitian conjugate, or sometimes the dagger of O, and is denoted 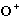. (That little "plus sign" should really look like a cross, but my word processor doesn't have that symbol!)

All the above words are stated mathematically as follows, we define 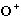by:

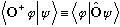for all functions phi and psi (!!!)

(I suppose it is not at all obvious that such a dagger operator even exists, but it really does for all operators O of interest to us. We will not prove it - it's getting into some pretty hairy linear algebra theory.)

If you star (complex conjugate) the expression above defining 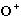, and remember from earlier that starring a bracket just reverses it:

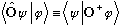(which is again true for all functions phi and psi.)

If you stare at this, you should be able to convince yourself that it means

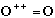. (Reminiscent of c**=c ?)

We can also write the definition of the dagger in integral form:

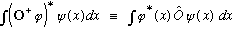for all functions phi and psi.

We talked earlier about Hermitian operators, we defined them before to be operators whose expectation values are always real. There is a very different definition of Hermitian operators, a more basic one, and we will see the connection between the two definitions later (we'll prove that they're really equivalent). Our new definition will be that

an operator, O, is Hermitian iff .

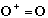Using our definitions above, this says that is O is Hermitian, then

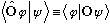for all functions phi and psi.

Hermitian operators are very special, and as we've already stated, they play a key role in quantum mechanics. (We'll see more reasons shortly)

Example 1:

O=c (Our operator is the "multiply by a complex constant "c" operator.)

Is this operator Hermitian?

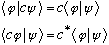
These two expression are not equal, unless c is real. So, the operator "3" is Hermitian, but the operator "i" is not.

It seems like a Hermitian operator might mean "real" in some way. This is sort of true: remember our old definition, O is Hermitian means <O> is real.

But you have to be a bit careful, the presence of "i" can be misleading:

Example 2:

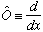, the derivative operator. It sure looks "real". Is it Hermitian?

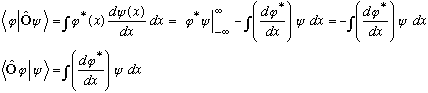
The signs disagree, the two lines are not the same. This operator is most certainly not Hermitian!

Example 3:

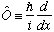, the momentum operator. Is it Hermitian?

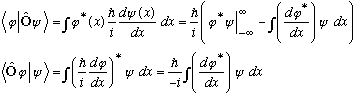
The explicit presence of an "i" has fixed up the minus sign. The two lines above agree, for any psi and phi, and thus this operator is Hermitian.

(We already argued before that momentum is Hermitian, using our old definition)

Example 4:

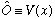. (This is the "multiply by a [real] function V(x)" operator.)

If V(x) is real this is just like case 1, the operator is Hermitian.

Earlier this semester, even before the introduction of Dirac notation, we used to write that the expectation value of O in a state psi is

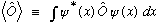
Now we see that the proper Dirac notation for this expression is

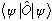, and the above is a pretty obvious shorthand notation!

Brief mathematical digression- Matrices

Go back to N-dimensional vector spaces, and define the operator O by 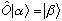We can understand what O does in general, as long as we know what it does only to our basis vectors!

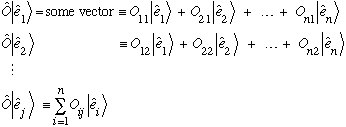
(Note the slightly screwy ordering of indices above - it's a definition!)

Given the above, how do I know what O does to ?

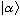Just expand 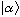, and you see

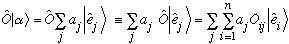
By inspection, we find

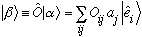, or in component form,

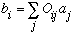
Now the ordering is making some sense, this looks like a matrix mult:

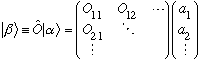
The N^2 elements in that matrix fully characterize the operator! If you know those N^2 numbers, you can figure out what O does to any vector! They are, unfortunately, representation dependent. If you change your choice of basis vectors, all the elements of that matrix can change.

This means that operators can be expressed explicitly as matrices, although the specific numerical entries do depend on the choice of basis vectors.

Once you've got this, you can work out products of matrices quite easily, e.g.

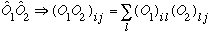
If you have a product of operators, just multiply the matrices!

And now, some definitions of matrix terminology:

Transpose:

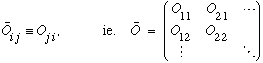
You can transpose a vector too,

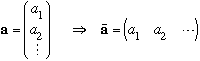
Conjugate:

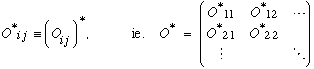
Adjoint: (or, Hermitian Adjoint)

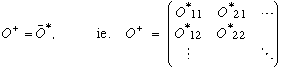
Which means

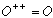
You can adjoint a vector too,

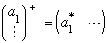
Note that our Dirac notation for vectors now looks like:

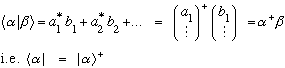
Which tells us in a more formal way what the "bra" is - it's the adjoint.

Still more definitions: Inverse:

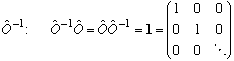
Unitary:

A matrix (or operator) O is unitary iff

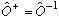
Hermitian:

A matrix (or operator) O is Hermitian iff

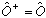
(This is the same definition as I gave above for vector operators)

If you write out the indices, you should not have too hard a time proving:

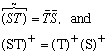
(An alternative proof, that doesn't make use of matrix indices, is this (using old "function" defs:)

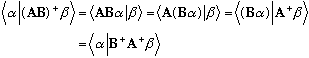
This is no matter what alpha and beta are, so it must be that )

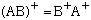Ridiculous Example:

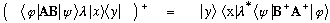
We've been defining operators in vector space, but as we've seen, we can continue with our analogy and now think about operators as matrices in Hilbert space. (They may, however, be infinite dimensional matrices, that's the price we pay!)

So, e.g. we can continue to use notations like

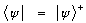
even though psi isn't really an ordinary column vector anymore!

Next time we will discuss the significance of Hermitian operators.

Here is the Next lecture