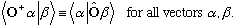
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 25 (Wed Oct 22, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

When we were dealing with operators, I had a rather different looking definition of the adjoint (also called the Hermitian conjugate) than the matrix one. My old definition, written now for vectors, looked like:

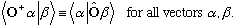
My new definition is .

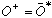Are these two definitions equivalent? Yes!

Using only the new matrix definitions we can derive the old definition:

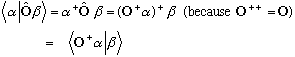
Ridiculous Example (again):

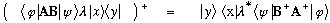
One immediate consequence of all the above is that we can often make quick proofs of important things, like e.g., we already know that momentum (p) was Hermitian. How about p^2?

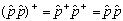
This statement proves that p^2 is Hermitian! (Stare at it, and convince yourself that you understand this quick and simple little proof.)

Since we just showed p^2 is Hermitian, and in an earlier example we showed that V(x) is Hermitian, it means that the Hamiltonian

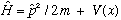
is also Hermitian.

What's the deal here? Why do we care whether an operator is Hermitian?

It's because of a few theorems:

1) The eigenvalues of Hermitian operators are always real.

2) The expectation values of Hermitian operators are always real.

3) The eigenvectors of Hermitian operators span the Hilbert space.

4) The eigenvectors of Hermitian operators belonging to distinct eigenvalues are orthogonal.

In quantum mechanics, these characteristics are essential if you want to represent measurements with operators. Operators must be Hermitian so that observables are real. And, you must be able to expand in the eigenfunctions (the expansion coefficients, as we have seen, give you probabilities!)

We proceed to prove these (I'll skip number 3, which will probably become fairly obvious, and the proof really doesn't teach us anything especially useful...)

Proof of theorem 1): The eigenvalues of Hermitian operators are real.

Let O be Hermitian, and write the usual eigenvalue eqn:

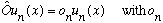some number, the eigenvalue of O.

In Dirac notation, we would write this equation as

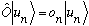
Now hit the left hand side with 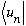, giving

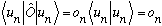
But, since O is Hermitian, then we also find

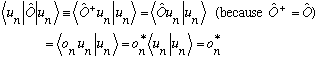
Combining with the previous expression, we see

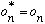
Which proves that each and every eigenvalue is real.

Proof of theorem 2): Expectation values of Hermitian operators are real.

Let O be Hermitian, and let 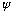be any state at all, then

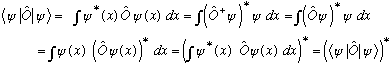
Comparing the beginning and end of that expression, we see that

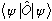must always be real, no matter what.

I can give you an alternative proof of theorem 2, which is a little cooler because it is "coordinate free", I never need to invoke functions in x-space:

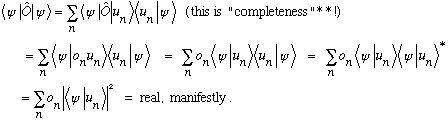
It's real because theorem 1 proved the o_n's are all real, and the absolute value squared of any bracket is always real.

(** This proof shows one of the nice uses of "completeness" - you can always stick 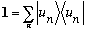into the middle of just about any expression. )

Proof of theorem 3) E-vectors of Hermitian operators span the Hilbert space. As I mentioned, we won't prove this one. (In the next theorem, though, we will prove it for a special case.)

Proof of theorem 4) The eigenvectors of Hermitian operators belonging to distinct eigenvalues are orthogonal.

Suppose I have two different eigenvectors of O, labeled 1 and 2,

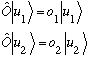
and suppose further that o_1 differs from o_2. (The e-values are distinct.)

Hit the 1st eqn. on the left with the bra <u2| , and hit the 2nd eqn with <u1|:

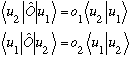
Now, star the second equation. What happens to the LHS?

.

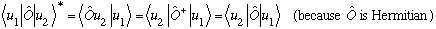Meanwhile, starring the RHS of the second equation gives

.

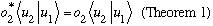Putting together the last two lines, we just showed that

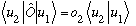
Above, we began with two equations, the first of which was

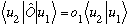
Subtracting these last two equations from each other, and recalling that o_2 and o_1 are by assumption different, the only way this can make sense is if

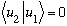, the two states are orthogonal. (As desired!)

In N-dimensional vector space, if all eigenvalues of O are distinct, there will be N of them [since O is an NxN matrix], and they're all orthogonal by the last theorem, so they must span the space (Theorem 3 is proven in this case). In Hilbert space, and/or if some eigenvalues are repeated, the proof is trickier, but still true.

Our formalism is mostly complete now. We'll be making lots of use of it, working out many examples where Dirac notation (and/or Hermiticity, the "matrix picture", completeness, etc.) will help us solve problems quickly and efficiently.

At this point, we're ready to try to pull everything we've learned so far this semester together, and summarize it all in some formal way.

Here is the Next lecture