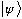Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 26 (Fri Oct 24, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

The postulates of Quantum Mechanics...

(1) The state of a particle is completely represented by a normalized vector in Hilbert space, which we call .

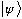(2) All physical observables, Q, are represented by Hermitian operators 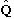, and the expectation value of Q in some state 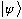is .

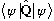(3) A measurement of Q on a particle in state 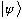is certain to return a particular value, 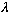, iff ("if and only if")

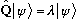
(i.e. if and only if 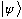is already an eigenvector of 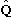, with eigenvalue )

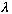(3a) If you measure Q (in any state 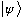), you are certain to obtain one of the eigenvalues of .

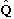The probability of measuring some eigenvalue 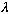is given by ,

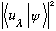(where 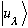is defined to be the eigenvector of 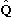, with eigenvalue .)

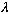(The above has to be modified slightly if there are degenerate eigenvectors. . It is always possible to arrange the set of 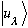's form an orthonormal basis, no matter what, but when we discuss degeneracy we'll see that it isn't always trivial. We'll talk about degeneracy shortly.)

(3b) After a measurement gives you the value 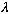, the system will collapse into the state .

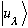(Again, modulo some subtleties if eigenvalues are degenerate)

(4) The time evolution of the state 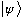is given by Schrodinger's equation:

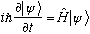
(These statements are a modification of Griffith's collection of the postulates of quantum mechanics. They are perhaps a little redundant (The statements 3a and 3b are closely related to 3, so I didn't give them separate numbers), and they are all consistent with one another. I claim that the above is pretty close to all you need to "derive" everything else in quantum mechanics...)

I would claim that statements 3b and 2 are also closely related, as follows:

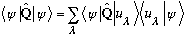(This is completeness, again, just math!)

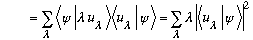
But postulate 3b says that 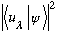is the probability of measuring ,

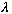so what we have written is equivalent to

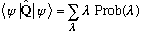, which is precisely what you would think the expectation value of an observable should be.

Digression: Some optional material about other representations:

[The following is a pretty intense discussion of how you pull explicit functions out of the abstract kets, which is in the end what we usually want. We will not be using this material directly, the next page and a half is meant for "reference" only!]

We're very used to thinking in the x-representation, i.e. I usually think of

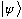as being equivalent to 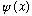. They are closely related, but 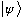is more general (it's like a vector V, while 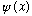is like the specific components

(Vx, Vy, Vz) in some particular frame.) Just as we can extract the components of a vector, we can also extract 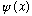from 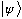. Here's how:

Consider the x operator, and it's eigenfunctions, which we'll call .

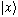To be specific,

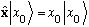
I normally use completeness to write 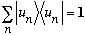, but now, with x having continuous (not discrete) eigenfunctions, I should write completeness as

.

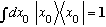Look at

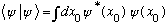
I can also use completeness to say

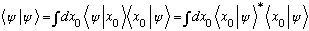
Comparing the two expressions, apparently

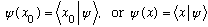
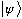is the general Q.M. state vector.

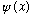is the probability amplitude fn for finding a particle at a location x

By postulate 3a, with Q=x, this is completely consistent:

Probability according to 3b is

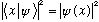
Completeness says that .

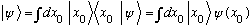Of course, I could equally well have chosen P as my operator, instead of x, with eigenfunctions u_p: 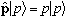 , in which case

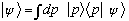
and I would know from Postulate 3a that

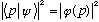= probability of finding momentum p.

This is telling me that

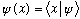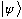: "What does the state look like as a function of x?"

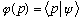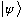: "What does the state look like as a function of p?"

It is interesting to ask what, e.g., 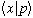is. (What does the eigenfunction of momentum look like, as a function of x?)

Recall that 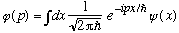, so I have

,

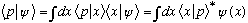comparing these tells me

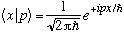
(We've seen this before! These are the eigenfunctions of p, written in x space)

Similarly, 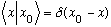, the eigenfunctions of x, i.e. 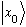, written in x space.

I can also write the above in the following equivalent pair of expressions:

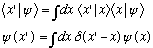
But we're getting awfully abstract, and we will not really need to use Dirac notation at such a level of sophistication for the rest of this semester - this is intended more to be in your notes to look at if you ever come back to this stuff in a grad class some day!

Degeneracy and simultaneous observables:

Suppose we have Hermitian operators A and B, each of which of course has its own complete set of eigenfns. Let's define the e-vectors and values of A:

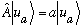
Suppose further that each and every eigenfunction 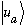is also an eigenfunction of B.

This might be possible, or it might not!

(We've seen that, e.g., the eigenfunctions of H are also all eigenfunctions of Parity, P, as long as V(x) is symmetric).

Anyway, if this supposition is o.k., then we have

.

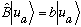But now observe the following:

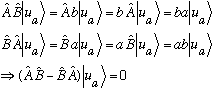
This wouldn't be all that interesting except remember that I'm supposing that it is true for each and every eigen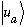function ! Consider what the commutator [A,B] does when acting on any old function, .

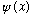A is Hermitian => the eigenfunctions of A span the space=>

we can expand 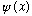in eigenfunctions of A =>

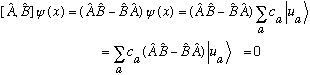
which means that [A,B]=0.

We say that A and B are compatible in this case. We can simultaneously know the eigenvalue of both of the operators, or we say A and B have simultaneous eigenvectors. (Remember, that was our starting assumption at the top - that every eigenfunction of A was also an eigenfunction of B.)

We have only shown that if A and B have simultaneous eigenfunctions, then they must commute. Does it work the other way? It does, although there are again some subtleties involved if there are degeneracies.

To see it work the other way, suppose [A,B]=0. Then:

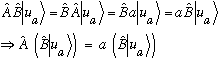
Stare at that last line. It is of the form A ("something") = a ("something"),

and implies that the "something" is an eigenvector of A, with eigenvalue a.

Now, if the eigenfunctions of A are non-degenerate, then each eigenvalue has by definition one and only one corresponding eigenfunction, implying:

.

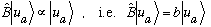Thus, if A and B commute, then indeed the operators will have simultaneous eigenvectors, but only if A has a "non-degenerate" spectrum.

What if A does have some degeneracy? Let's suppose for simplicity that it is just 2-fold, i.e.

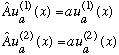
Knowing (as I showed above) that 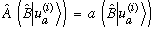merely tells me that 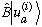must be some linear combination of .

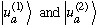The Gram-Schmidt procedure is what you use here two find 2 orthogonal combinations of 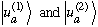which are themselves eigenfunctions of B.

(They might be degenerate in B, or might not be.) Gas. works it out on p.123.

Bottom line: If [A,B]=0, then (even if A has degeneracies), we can still always generate an orthogonal basis of vectors which are all simultaneously eigenfunctions of B as well.

If we are unlucky, and some degeneracy in B still exists, there must be a 3rd operator, C, which satisfies [A,C]=[B,C]=0 and now we can find an orthonormal basis which are simultaneously e-fns of A,B, and C, and (hopefully) with distinct eigenvalues for operator C. (If not, you may need a D, and E, etc...) At some point, you will have a set of operators, A, B, C, ... M, which all commute with each other, and which have a common set of eigenfunctions, and each and every such eigenfunction will have a distinct set of eigenvalues.

This set of operators (and eigenvalues) completely characterizes any wave function:

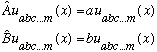
etc. , and the set of numbers a,b,... m characterize the state fully.

What if [A,B] is not zero? Then, we cannot simultaneously know the eigenvalues of A and B, in general. Next time, we'll quantify this:

Here is the Next lecture