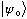Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 27 (Mon Oct 26, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Pick a state, 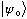, any state. Define the uncertainty of an operator, A, in that particular state in the usual way we have all semester:

,

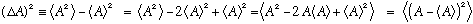The Schwartz inequality is a completely general theorem, which says

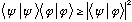for any phi and psi. (Kind of looks like (1)(1) >= )

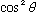Next, we define a particular psi and phi (which, like anything, will have to obey the above Schwartz inequality):

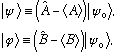
Observe:

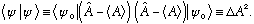
and, similarly,

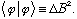
So the Schwartz inequality for this particular case reads

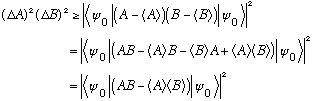
But we know expectation values of Hermitian operators are always real. And we can also write that the square of any complex number z obeys the following inequality:

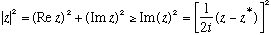
Making use of this in our last expression we find

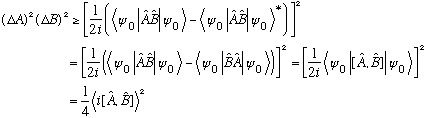
If [A,B]=0, then we just showed basically nothing at all, we have the trivial identity

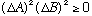
(Which implies that you could know A and B both, simultaneously)

However, for x and p, where we have

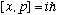
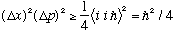
i.e.,

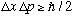
x and p are incompatible observables. (Incompatible observables do not share a complete set of common eigenvectors)

We have just derived the Heisenberg Uncertainty principle purely by using operator properties. There was no discussion of waves, or wavefunctions, or Fourier transforms, or anything! It depends only on the observed properties, and not on the particular object which you are looking at!

Final topic of Ch. 6: Time dependence

Consider the time evolution of the expectation value of any operator, O:

.

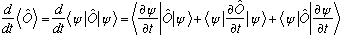The Schrod equation tells us what the time evolution of wave fns is:

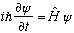
Putting this into the first equation gives

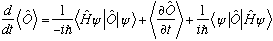
But H is Hermitian =>

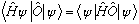
We thus have

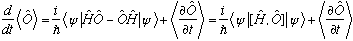
Most operators don't have any explicit time dependence, so that last term generally vanishes! (E.g. if O is x, or p, or p^2/2m, or V(x), or Parity, or anything like this, the last term vanishes.) It's only if you explicitly see a "t" in the operator that you must include it, like e.g. if you had a potential which looked like V= 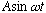, or something...

Example 1:

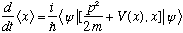
[V(x),x]=0, and it's not hard to work out 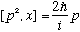which means

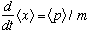
Our old friend!

Example 2:

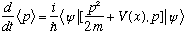
This time, [p^2,p]=0, and we need to work out [V(x), p]:

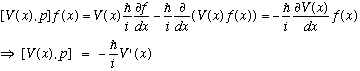
In this case,

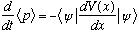
which is Ehrenfest's theorem. This was an extra credit problem on an early homework: proving it directly using Schrodinger's equation (integrating by parts repeatedly) was a big pain, and took over a full page of algebra in my solutions. With this technique, it's an easy 2 liner!

Example 3:

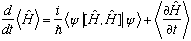
Clearly, any operator commutes with itself. So, unless the Hamiltonian has an explicit time dependence (e.g. an explicitly time dependent potential), the expectation value of energy is conserved, as you would certainly hope!

Here is the Next lecture