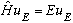Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 28 (Wed Oct 29 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Gas Ch. 7 - operator methods.

One lesson to carry away from the previous chapter is that operators (i.e. observables) play a big role in Q.M. E.g, the Heisenberg uncertainty principle was derived with no mention of the wave function, but only looking at the properties of momentum and position operators. This is a very new idea - earlier this semester, the wave function seemed like everything! Let's now look at an old problem in a new way, and emphasize the importance of operators in the final result.

We revisit the Harmonic Oscillator, where (as always) we want to find the eigenvectors and eigenvalues of the Hamiltonian, 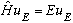, with

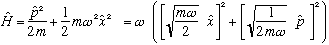
In the 2nd expression, I merely rewrote the 1st, messing around a bit with the constants, to put it in a form that looks like u^2+v^2. In the world of complex numbers, a sum of squares factorizes simply: u^2+v^2 = (u-iv)(u+iv). We shall see later that writing H as a product like that might be very handy. (For right now, you may want to sit back and watch the following algebra unfold with some sense of just-barely-motivated mystery. I find it a bit hard to imagine how someone thought of this whole business the first time around, although once you see where it leads to it's so handy, useful, and clever that it may even seem "intuitive" looked at after the fact!)

H sort of looks like it factorizes, but that's not exactly right, because u and v (which in this case are proportional to x and p) are operators, and so don't commute. You have to be careful not to assume simple algebraic relations when you have noncommuting operators! Remember, .

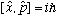Still, the form of the sum of squares sure suggests factorizing. So, let me go ahead and simply define some new operators, that look basically like "u+iv" and "u-iv"... (I am going to stick in an extra factor of Planck's constant, for later convenience. These are defined quantities, after all) So I define operators

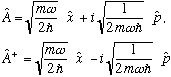
The second line is just the "dagger", or Hermitian conjugate, of the first. Since x and p are themselves Hermitian, all this does is flip the sign of "i".

Remember, our initial guess was that H = (u-iv)(u+iv). So, let's simply examine what 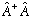is. It will almost give us H, just not quite:

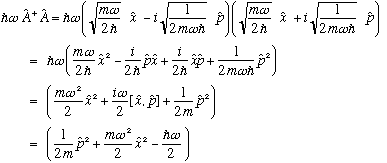
Not bad! This expression is indeed almost identical to H. Except for the last term (which arose from the fact that x and p don't commute) But that's ok, the last term is just a constant number, so we have

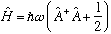
Notice the relative order of A(dagger) and A. It is important! Order matters whenever you are messing with noncommuting operators. (xp and px are quite different) If instead, we had done them in the other order we would have found (convince yourself!)

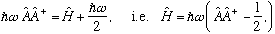
It looks almost the same as what I had, but reversing the order of the A's also means flipping the sign of that additive constant. It's easy to see

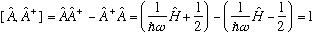
(Or, you could prove this directly, straight from the definitions of A and A(dagger), using the commutation relation for x and p.)

B.T.W., if you ever need it (and you may) it's very easy to get things like [H,A]. Just use the identity

[XY,Z] = XYZ-ZXY = XYZ -XZY+XZY - ZXY = X[Y,Z]+[X,Z]Y

which we use to find e.g.

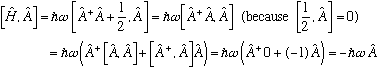
Now, here comes the essential trick: If some eigenfunction u_E(x) solves the Schrodinger Eqn, with energy E (i.e. 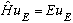) then I claim that the function Au_E(x) also solves the Schrodinger. Eq, but with a different energy, .

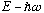Proof:

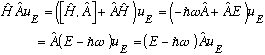
Compare the first and last bits of the above, we have just shown

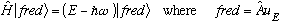
which means, as claimed, that Au_E is an e-fn of H with e-value .

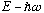Of course, there's no way we can tell whether Au_E is properly normalized. We'll have to fix that up later.

The above result is much cooler than it might at first glance appear. What I have done is given you a "machine" (the operator A) which can be used to find new solutions. If you know one eigenfunction, you apply A, and you will get another, different, solution to the Schrod Eqn! (And you can keep repeating, to get more and more solutions)

In exactly the same way, I claim that 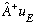also solves the Schrod. Eq, only this time it has an energy

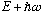
Proof: (Goes just like the proof above)

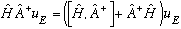
But note that

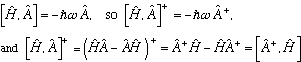
which means 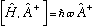and thus plugging in the 1st line of our proof:

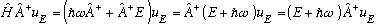
which, just as above, means that 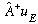is an e-fn of H with e-value .

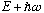A and A(dagger) are sometimes called "Ladder operators", because they allow us to climb up and down in energy, by steps.

A(dagger) is also called the raising operator, and A is called the lowering operator (for obvious reasons)

But there's something funny going on here. Say I have some particular eigenfunction (any one at all), call it 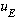. Now start applying A to it. I will (by the above proofs) keep finding new eigenfunctions with lower and lower energy, stepping down by the fixed amount 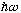each time. Eventually, I will find a state with a negative energy. (!?) But that's impossible - my potential is everywhere positive, and KE is always positive: negative energy is not possible in this potential. I can prove this in a more mathematical way too:

Proof:

For any Hermitian operator O, the following is true:

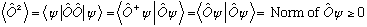
which means 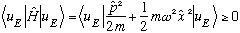, as I claimed

Conclusion? We appear to be in trouble, since I proved that Au_E is always a solution to the S.E.. But wait... What if Au_E=0? This still "trivially" solves the S.E., but from then on operating A again and again would just keep giving me zero. (Which means, I would not generate any more solutions with lower energy) This is the only way out, it must happen, otherwise we'd have an impossible negative energy solution!

So as I continue operating A on valid solutions, over and over, lowering the energy step by step, I must reach some last, lowest, nontrivial (nonzero) state, which I will call 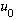. The arguments just given say that A 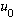=0. (It must be, because we've shown that if it's not zero, then it's an eigenvalue of energy with lower energy, and yet by hypothesis 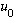is the lowest state.)

What is the energy of this lowest state? Just remember what I showed a few pages ago, namely 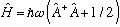. So what happens when I operate H on this state 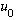? I get

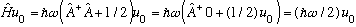
Which shows that the state 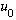is indeed an eigenfunction of energy (as postulated!) with energy .

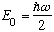This is nice! We have found the ground state energy of a Harmonic Oscillator without doing any power series or Hermite polynomial stuff, or anything. We merely used our lowering operator idea.

Also note: If you hit 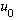with A(dagger), you will get a new eigenstate 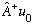(it won't be normalized, but after I normalize it, I'll call it u_1), and the energy of this state (by our first little proof above) is going to be 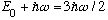. And, hitting this eigenfunction again with A(dagger) gives yet another state (after normalizing, call it u_2) with energy 5/2 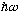. And so on. We have now found all the allowed energies, not just the lowest one. (E_n = (n+1/2) 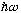) All "for free"! It comes from operators and commutators.

The only thing remaining to do is to figure out what exactly the function 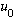(x) is. But that's easy. Remember the equation we found above, A 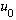=0

Let's solve this:

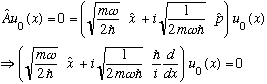
This is a simple, first order linear differential equation. It has a unique solution (with one undetermined constant of integration, which is fixed by normalizing) The solution is:

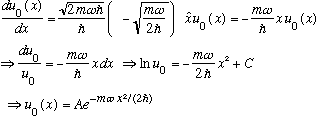
You can normalize this one "by hand" (square it, integrate it, use the Gaussian integral we know so well - you've done this as a hw problem.):

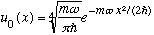
We have found the ground state wave function, as well as its energy, all without having to do any nasty power series, or asymptotic arguments, or anything. And, our raising operator acting on this function will start us up the ladder of all the other solutions.

Here is the Next lecture