CURrENT Electrodynamics Assessment
The Colorado UppeR-division ElectrodyNamics Test (CURrENT) is a free-response assessment on basic topics from junior-level electrodynamics, where the focus is on gauging student understanding of fundamental concepts, and whether they can complete basic advanced E&M tasks. The post-assessment can be completed by students in less than 50 minutes; the pre-instruction version can be done in less than 15 minutes. The questions were written to reflect both the broad and topic-specific learning goals expressed by experienced physics faculty. The topic coverage in this assessment is limited to core material that is likely to be taught at most institutions, since we’ve found there to be some variance due to institutional peculiarities. [See: "Topics across institutions"] We provide below some notes on its implementation, and on the overall design and validation of the assessment.
The pre- and post-instruction assessments (along with detailed descriptions of individual questions, an analysis of student responses from two recent implementations, and comments on student difficulties) are available in a zipped file, but the download is password-protected ( if you want access). If you choose to use these assessments in your own course, we would be happy to provide feedback on student responses from your institution, with a reasonably quick turn-around time.
| I. Notes on Implementation |
| II. Notes on Design |
| III. Preliminary Results |
I. Notes on Implementation
Post-Instruction: The assessment requires at most 45 minutes for students to complete. It should be given in the week or two before the end of the term, or at least after all the topics it addresses have been covered.
Ideally, instructors would not announce before that day’s class that students will be taking an assessment – this is to encourage full attendance and to discourage studying beforehand, since we would like to gauge their general retention, and get as large a sampling of the student population as possible. If instructors do announce this beforehand, they should encourage students to look at this as a review for the final, that can be used as a guide to future studying, to decide where they should concentrate their efforts.
CU SP12 students knew of the assessment beforehand. We took a few minutes at the beginning of class to introduce the assessment, in particular to remind them that their performance would not impact their final grade in the course, and that they should see it as a chance to prepare for studying for the final. We saw that a few students were discouraged by their poor performance, so we feel it’s important to emphasize that this can be a learning opportunity for them.
In other words, we wanted students to try their best to answer the questions completely, but to not worry about any possible repercussions for blanking on an answer. In the spirit of this, we would encourage instructors to provide some kind of feedback to students on their performance, at least to those who ask for it, in terms of what areas they can improve on. At the same time, we request that you not provide written solutions to students under any circumstances, and we suggest they be told the reasons for this up front.
An earlier (very similar) version of this assessment was given at two different institutions in the SP12 semester, and on both occasions every student finished within 45 minutes; the fastest were through after ~25 minutes, with most being done inside 40 minutes. This current version differs from the previous in only minor details (there has been some slight re-wording of a few problem statements for the sake of clarity), so we are fairly confident about the time estimate.
Pre-Instruction: This should take at most 10-15 minutes for students to complete; it has been given at two separate institutions, in both cases on the first day of class. As with the post-instruction assessment, we feel it’s best to encourage students to see this as a review of some first-semester material that will be useful in the coming semester, which can help them gauge what they may have forgotten over the break. Again, it is certainly appropriate to provide feedback to students, but we ask that instructors not provide students with written solutions to the assessment questions.
II. Notes on Design
The Colorado UppeR-division ElectrodyNamics Test (CURrENT) is an assessment of fundamental skills and understanding in core topics from advanced undergraduate electrodynamics. The basic (though not introductory-level) nature of these six multi-part questions reflects our premise that a more sophisticated understanding of advanced E&M is unlikely for students who haven’t yet mastered essential concepts. Its open-response format follows from an expectation that more advanced students should be able to generate their own answers, and to justify their correctness. The focus is conceptual, though some mathematical manipulations are required (per our learning goals)
At the outset, we searched for existing assessments that would be appropriate for junior-level electrodynamics students, and found only one: the multiple-choice Electromagnetics Concept Inventory (EMCI), written by Branislov Notaros (currently at Colorado State University). There are several designed for introductory courses, and two for upper-division electrostatics: the Colorado Upper-division Electrostatics (CUE) Assessment; and a multiple-choice by Chandralekha Singh covering Gauss’ law and symmetry – the latter was written for introductory courses, but could also be used in an upper-division course. Please contact us if you are aware of others. [See: http://www.ncsu.edu/per/TestInfo.html for a detailed list of physics assessments.]
The pre-instruction assessment contains three questions that are nearly identical to their post-instruction versions. Two questions have had the time-dependence removed, so that they are doable with knowledge of first-semester material, but still roughly comparable to how they appear in the post-instruction assessment.
Our biggest concern along the way has been with length – we wanted an assessment that was appropriately difficult for an upper-division course, but could still be completed by most students in a 50-minute class period. This provided further incentive for limiting questions to the most basic topics, and to focus on problems requiring little or no direct calculation to answer. We restricted topics to those we could reasonably expect to be covered in most electrodynamics courses at other institutions. So, for example, relativistic electrodynamics is not covered, since many institutions teach undergraduate relativity in separate courses, or give sparse or rushed coverage at the very end of the semester. We’ve intended the questions to be simple enough that any instructor would agree they would want their students to be able to answer these questions without difficulty by the end of the course. Most of the questions are still challenging for junior-level students, and the few questions with very high rates of correct responses are being considered for revision, although incorrect responses to these questions have still provided interesting insights into student thinking. The questions will for the most part stay in their current form, at least until we’ve had more opportunities to implement them at other institutions, particularly ones taught in “traditional” settings.
Earlier versions of this assessment proved to be too long and too difficult – we found we were often overestimating what students knew or could do within the allotted time and format. For example, we originally thought it would be too trivial to ask whether the EM energy density is increasing inside a solenoid when the current is increasing (the field is increasing in magnitude, so naturally the energy density must be increasing), but instead found that many students were still unclear about what the magnetic field looks like inside (or outside) a long solenoid, a few even thinking that the field is zero inside and non-zero outside.
The earliest version of this assessment was tested with two student interviews and then administered at the end of the FA11 semester at CU; it turned out to be too long and difficult for most students to complete within 50 minutes. After dropping one of the questions and re-wording others, the second version was pre-validated with five individual student interviews (a few small modifications were made), and then given at two separate institutions at the end of the SP12 semester. This second version was completed by every student within the allotted time. The latest version incorporates a few slight modifications (based on the SP12 student responses and five post-assessment student interviews, as well as feedback from the instructors); other small modifications may be made after further implementations and validation interviews.
III. Preliminary Results
The CURrENT was given in SP12 at CU (N=24), and also at a small, selective engineering college (“X”; N=11). Instructor X was present at our summer meeting in 2011, had access to the FA11 CU course materials, but did not use the guided in-class tutorials. Students in both courses were encouraged to not study for this ungraded assessment, and instead use it to judge their understanding before preparing for the upcoming final exam. Responses from both institutions were scored using a consistent rubric, and the average CU SP12 scores were significantly higher for Q3 and Q4 (p ≤ 0.001), and for the total score (p < 0.05). [See figure below.] Scores were not significantly different for the other questions, though X-students performed better than CU on Q2, regarding the fields produced by a time-varying solenoidal current.
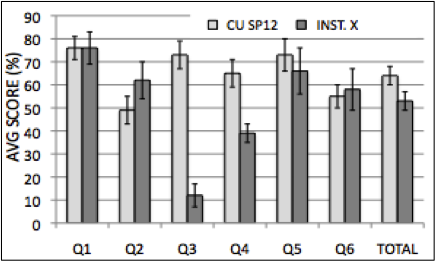 |
Average CURrENT scores (by question and total) for CU SP12 (N=24) and Institution X (N=11). Significant differences are seen in Q3 & Q4 (p ≤ 0.001) and the total score (p < 0.05). Error bars represent the standard error on the mean. |
The relatively high CU SP12 results for Q4 (which asks students to transform a curl equation to its integral form via Stokes’ theorem) can be attributed (at least in part) to our emphasis on the equivalency of the differential and integral forms of Maxwell’s equations, and on the coordination of lines, surfaces and volumes when applying the integral forms. 13/24 of our students were able to correctly and completely explain each of their three steps in this short derivation; only 3/11 X-students reached the final result, though none of them offered complete and correct reasoning for each and every step. Instructor X reported that he hadn’t reviewed the Divergence and Stokes’ theorems since the first semester.
Q3 (which concerns the current density inside a radially-decreasing wire carrying a steady current; see figure below) can be answered without any calculations, but requires an understanding of the microscopic version of Ohm’s law (J = σE), boundary conditions on electric fields, and conservation of charge. These topics are directly addressed in many of the clicker questions (as well as several of the tutorials), and most SP12 CU students answered both parts of this question correctly. However, 10/11 X-students incorrectly thought the divergence of J would be non-zero inside the wire (the remaining student left this question blank), because the magnitude of J is increasing to the right. At least half of them were distracted by the appearance of “converging” field lines, which they took to represent a non-zero divergence. Only 1/11 X-students could correctly explain why the electric field just outside the current-carrying wire should be non-zero (the parallel components of the E-field are continuous across any boundary, as required by Faraday’s law; there are also surface charges, which are responsible for the uniformity of the current inside the wire). Student reasoning was varied here, though several incorrectly applied Gauss’ law to argue that the electric field in the region just outside the wire is zero because the charge density there is zero. This is consistent with our observation that E&M II students may still sometimes think that a vanishing divergence (or line-integral) of a field implies that the field itself is zero.
 |
Diagram from Q3 of the CURrENT, showing a radially decreasing wire that carries a steady current density J. The parallel components of the E-field are continuous across any boundary, making the field non-zero just outside the surface of the wire. Div.J = 0 inside the wire by charge conservation (or, the continuity of the field lines). |