Physics 3220, Fall '97. Steve Pollock.

Gas. Ch. 11 - Angular Momentum

3220 - Notes, lecture 37 (Wed, Nov 19, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

(as usual, these notes will be modified after the lecture to reflect the true starting and ending point)

Last time, we explicitly solved for the phi dependence of the Ylm's, and in doing so, found the eigenfunctions of L_z. We can already make some use of this result:

Example: A rotating solid object.

Classically, a rotating solid object, spinning about the z axis, has E= .

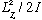Equivalently (since V=0), we have .

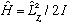But the eigenvectors of L_z and L_z^2 are the same, so we can instantly solve the Schrod Eq:

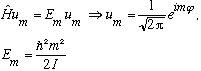
Note: this rotating object has a degeneracy, (m and -m give the same energy) which corresponds to rotating clockwise or counterclockwise!

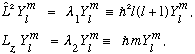
We have already found the solution to the L_z equation, so we only need the eigenfunctions of L^2. Now for the unmotivated but useful and important trick! We are going to define new operators, which will play the role in the angular momentum world that A and A(dagger) did in the H.O. world- raising and lowering operators. They are

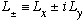
Again, Gas. works out very explicitly what these new L+/- are in spherical coordinates, but you can also use my little picture on the previous page to get it, perhaps more easily/geometrically. Let me 1st explicitly write out the two angular unit vectors (which I get by inspection, can you convince yourself these formulas are right?)

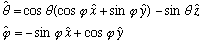
Then, I'll use these when I dot L with x and iy and add up to get

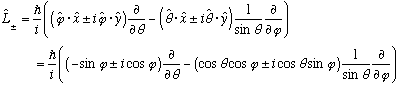
Summarizing,

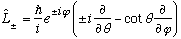
We will use this (explicit) form every now and again. But more often, we will be interested in various expressions more suitable to operator methods!

E.g.:

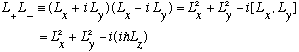
(where I made use of the commutator of L_x and L_y, derived in Ch. 10)

Solving for L^2:

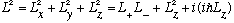
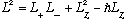
We could write this out in terms of theta and phi, since we have explicit forms for L+, L-, and Lz already (We effectively did this earlier.) But it turns out we really don't need to do this. To solve for the eigenvalues of L^2 and L_z (the spectrum), and also the eigenvectors (the Ylm's), the operator way, we are going to need some trickery analogous to our discovery in Ch. 7 of A and A(dagger), their commutator [A,A(dagger)], and the commutation of [H,A]. Let's set that up:

We already observed that

.

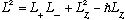Following how that proof went, you can easily check yourself that

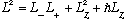
Subtracting these two equations gives .

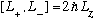Also, making use of our old result, 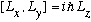(and other similar ones)

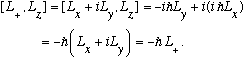
An entirely analogous proof (you can check this yourself) shows

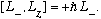
We saw in Ch. 10 that [L^2,L]=0, so

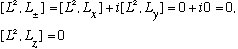
These relations are all we need. Here's the first important thing to notice:

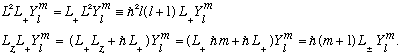
Staring at these two equations, we discover that e.g.

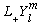is an eigenvector of L^2 with the same eigenvalue as Ylm had.

But 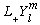is an eigenvector of L_z with a different eigenvalue, namely

!!

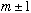Similarly, you can quickly see that

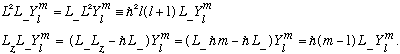
What we've just found is that L+/- are "Raising" and "Lowering" operators for L_z. (And they don't mess up L^2 at all.) We can write

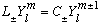
(C might depend on both l and m, and there's no reason it must be 1.)

Can we keep on raising m forever? No!

Proof:

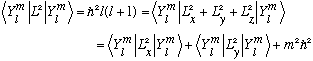
(Where I have made use of the fact that the Ylm's are normalized.)

L_x and L_y are Hermitian (can you see how to prove this? Look at the definitions back in notes 9/10-8.) You proved on a hw that this makes

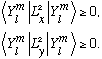
Putting this together, we find

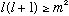
m is bounded from above (and also bounded from below)! You cannot keep increasing m by 1, forever. This means there must be a final state, with maximum m. Call it .

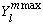It must be true that 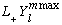=0, because otherwise we'd have found 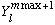, which we just proved was impossible.

Here is the Next lecture