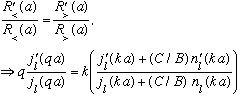
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 36 (Mon, Nov 17, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

We will name the solution when r<a, "R<", and the solution for r>a, "R>".

Continuity of both R and R' says

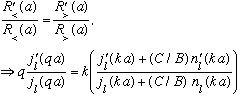
Since we are given V0 and E, we already know q and k, and this equation has only one unknown: (C/B). (It depends on k, of course) A neat property of spherical Bessel's is that for large arguments, you find

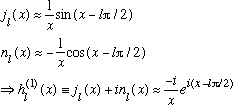
(The last line defines another function, called the spherical Hankel function, which is just a linear combination of Bessel's and Neumann's.)

Our solution, for large r is then

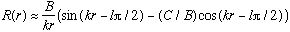
We can rewrite this in several other equivalent forms, e.g. (still for large r):

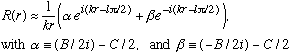
The first term looks like an outgoing spherical wave, the second term looks like an incoming spherical wave.

Or else, we can rewrite it as (still for large r)

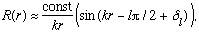
where 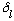is a phase shift (not a delta function of any kind!)

N.B. This phase shift is easy to write in terms of B and C:

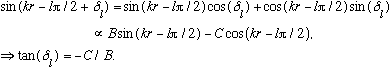
Apparently, the phase shift depends on k (since C/B does)

The "constant" is just normalization, we won't worry about it.

If V=0, then C must be zero, and thus the phase shift is also 0.

In this case, again for r>>a,

,

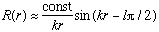which is equal parts incoming and outgoing waves.

(The incoming wave "bounces" off the wall at r=0, and makes an equal amplitude outgoing wave, in the steady state)

If V is not zero, we have just seen

.

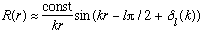This means that far away, the wave function really looks about the same, whether there's a potential well there or not. Except for the phase! The phase tells you there's a potential. Experimentally, if you scatter two particles, all you can really do is measure |psi|^2 far away. But doing this (in principle) can tell you what 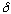is, and thus you learn something about the potential. This is one way nuclear and particle physicists learn about interaction potentials of particles. ("collision theory")

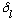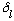N.B> If >0, the scattered wave is "shifted in", and this generally occurs if V0<0. If <0, the scattered wave is "shifted out", and this generally occurs if V0>0. See Fig. 10-3 and 10-4 in Gas, for a very helpful plot of this when l=0. There is a simple physics explanation for this:

If V0>0, there is less kinetic energy available inside r=a. So, there is less momentum, which means the DeBroglie wavelength is longer in there. So, the wavefunction must be stretched out inside the well, and you see that outside: the wave function has been pushed a bit to the right. (The opposite happens for attractive wells, and the sin gets pulled in)

Next example: Finite well, but E<0 (3-D bound states)

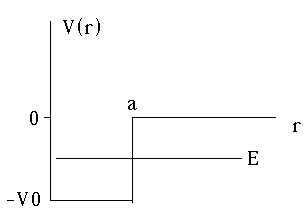
As usual, our radial equation looks like

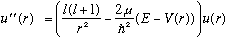
Inside the well, things are basically the same as the previous problem, and we define

.

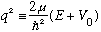The solution inside (as we have seen several times now) is

.

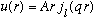But outside, we have something just a little different:

.

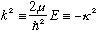We now want imaginary arguments in our spherical Bessels! It turns out that only one special linear combination of j_l(ikr) and n_l(ikr) goes to zero as r gets very large, namely that spherical Hankel we defined before (only, with an imaginary argument):

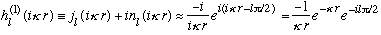
(The last two expressions are only true for large r, but they show that the function is indeed well behaved at infinity)

You must match the Bessel function j_l(qr) with the function

h_l^(1)(ikr) at the point r=a (both value and derivative). This will put a constraint on kappa, and thus E. It will, in fact, quantize E. But, it's a nasty ugly equation if l is not zero, and we will leave it be!

This concludes our first survey into solutions of the radial equation. We have found solutions for the infinite and finite wells, bound states and scattering states. There's a lot of physics in this! We have not explicitly talked about the free particle in 3-D, but it's really a special case of what we've done (with V=0), and you can read about it in Gas. pp. 178-180.

The other two extremely interesting and important cases are the Hydrogen atom bound states (with V(r)=-Ze^2/r), and the 3-D Harmonic oscillator, with V(r)=(1/2)kr^2. We will solve the hydrogen atom in Chapter 12, and leave the Harmonic oscillator for homeworks. But before we do this, it will be nice to go back to where we left off around p.(9/10)-10, and revisit the angular equations, and study angular momentum a little bit more carefully.

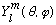Remember, we didn't really ever solve for the part of the 's.

I merely quoted some results regarding associated Legendre functions (p. 5 and 6), but didn't derive anything. Just as with the 1-D harmonic oscillator problem, where we basically quoted the results of solving a complicated "special function" 2n'd order ODE, and then went back and figured it all out using operator methods - we'll do the same thing here!

This concludes Ch. 10, next we begin

Gas. Ch. 11 - Angular Momentum

We have already learned that the solutions to the angular part of the Schrodinger Equation in spherical coordinates, the 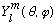's, are also eigenfunctions of both L^2 and L_z. This gives us a handle to study/derive these functions in a far more elegant way than the rather "brute force" solution from Ch. 10. There, we invoked the solution of a (perhaps unfamiliar) second order ODE. (It's going to be somewhat analogous to our treatment of the Harmonic oscillator, involving tricks with ladder operators!)

We are looking for fns which simultaneously satisfy the eigenvalue eqs:

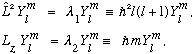
I have given explicit names to the eigenvalues, pulling out the units, and using names which I claimed before will ultimately make sense. For now, the names (l(l+1) in particular) may look arbitrary and unmotivated.

Recall from Ch. 10, (notes, 9/10 page 10)

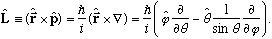
Simply dotting the above with z gives the z component of L:

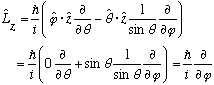
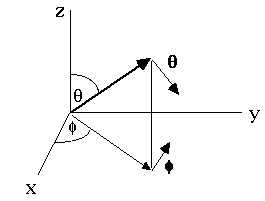
I got those dot products by drawing a little spherical coordinates picture and staring. Try it yourself, and convince yourself that 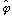is perpendicular to z, and

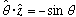
You can look at Gas. p 189 for a grungier proof, if you like!

Remember our goal is still to solve

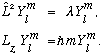
I should also remind you that the second of these two eigenvalue equations is easy to solve:

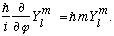
You can simply separate variables, i.e. write 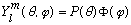, plug this in, divide out P(theta), and immediately find

.

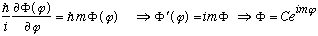As we argued before, this wave function should not change when phi increases by 2pi, which implies m must be an integer. (Also remember that m being a 1/2 integer might also work, if we don't mind the sign of phi being different when you run around a circle, but we're going to ignore this slightly crazy looking idea for now)

Let's also explicitly normalize it:

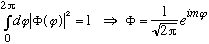
But we really already knew this - the phi equation was easy to solve right from the start. It's the theta equation, i.e. the eigenvectors and eigenvalues of L^2 that we've been sort of dancing around.

Here is the Next lecture