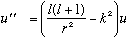
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 35 (Fri, Nov 14, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

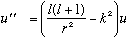
is

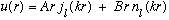
where j_l is the spherical Bessel fn, and n_l is the spherical Neumann fn.

The functions can be found by the following general formulae:

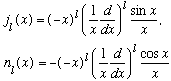
or more specifically,

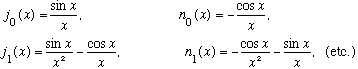
Note that if you set l=0, you get u=Asin(kr)-Bcos(kr), just as we had found.

Spherical Bessels are finite at r=0, but Neumann's blow up like 1/r^(l+1)

So the solution, r j_l(kr) goes to 0 nicely as r -> 0, but r n_l(kr) is finite (or infinite) as r->0, neither of which is acceptable. Thus, we must have B=0.

Our solution is then

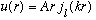
u(a)=0 still must be true. So plugging this is we find A a j_l(ka) =0.

Thus, k is constrained. Indeed, ka must be a zero of the lth spherical Bessel.

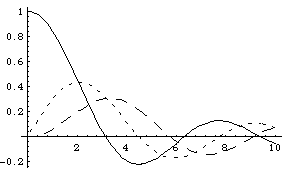
Here are plots of j0 (solid),

j1 (short dash), and

j2 (long dash)

These fns are kind of "sin"-ey, but not exactly. They do have an infinite number of zeros, but the function damps away, and the zeros are not evenly spaced out (except l=0.)

If you call the nth zero of the l'th Bessel function 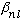, we have

.

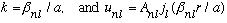Finally, the total wave function is

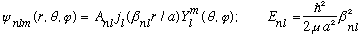
(The A_nl can be found by normalizing. )

Note that (Boas proves this) if n' is different from n, then

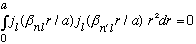
Which says the wave functions are orthogonal if n and n' differ, even if l and m are the same. (If l and/or m differ, the wave functions will be orthogonal due to the angular integration over the Ylm's. )

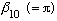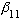The lowest zero of any of the Bessel fns is . (Because this is l=0, we call it an "S" state, and this is the first out of all the Bessel's zeros.) The next lowest zero of any Bessel fn is (Because this is l=1, we call it a "P" state. This is the first zero of the l=1 Bessel.) The next zero of any Bessel fns is 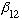( l=2, "D" state, first crossing.) Before you think you can predict the pattern, beware. The next zero of all the Bessel functions is now the second zero of the l=0, or "S" state, .

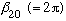These results tell you what happens if you start sticking electrons into an infinite, spherical box (or, roughly, protons and neutrons into a nucleus!)

You will first fill up the 1s state. This is non-degenerate. (Spin => 2 protons)

Then you fill up the 1p state. (3 fold degenerate, 6 protons. Total is now 8)

Then the 1d state. (5 fold, 10 protons, total is now 18). Next, comes the 2s state (non-degenerate, 2 protons more => 20) These are "Magic nuclear #'s"!

Next example: A finite square well in 3-D

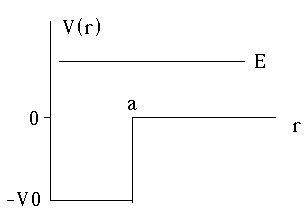
So, V(r) = -V0 (r<a),

0 (r>a)

As usual, in 3-D, the effective potential goes to infinity at r=0, so as to force u(r=0) to 0.

We will first consider E>0. This means free particles, or continuum solutions.

We know from 1-D that E>0 means E is not quantized. You can pick it!

The physics here is of two attractive particles which scatter from one another. (Or, a single particle hitting a fixed attractive center, and scattering off it)

The radial equation, as usual, looks like

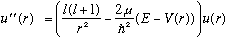
When r<a, we define

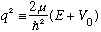
Then the radial equation looks just like the one we solved in the previous example (except for the switch of symbol k for symbol q)!

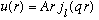if r<a.

(The n_l solution is, as before, no good when r -> 0)

When r>a, we define 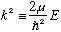, and again the radial equation looks just like the one we solved in the previous example, and

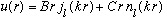when r>a.

Note that we have no reason to throw away the n_l term this time, because this solution is only valid for r>a, so there's absolutely nothing wrong with the n_l function!

Now, let's switch back to R(r)= u(r)/r, to get ride of the irritating "r" factors (remember, R(r) is the true radial wavefunction anyway, we just defined u(r) so that our effective radial equation would look like the old 1-D one.)

Of course, R(r) must be continuous everywhere (including r=a), and the same goes for R'(r). (Just like in 1-D, otherwise the S.E. doesn't make sense)

We will name the solution when r<a, "R<", and the solution for r>a, "R>".

Next time, we will show what continuity of R and R' says.

Here is the Next lecture