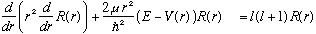
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 34 (Wed, Nov 12, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

For now, let's go on to solve the radial equation (finally!) for a couple of simple (looking) cases: You can go back to our original equation, or do the separation of variables as outlined on the previous page. Either way, we need to solve the radial equation:

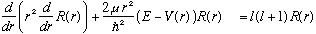
which we can also rewrite in the equivalent forms

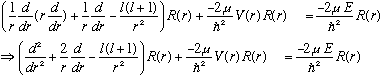
What labels should R have? It clearly depends on l. It clearly does not care about m. But this is an energy eigenvalue equation. So, we could call it

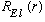. In anticipation of quantizing E, we call it .

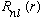In general, most potentials vanish (or can be defined to vanish) as r -> infinity. Let's also assume that R(r) is well behaved as well. This means that it should vanish at infinity, so the normalization integral

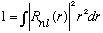is o.k.

Also, it should not blow up at r=0. It doesn't have to vanish, but it should stay finite. It turns out to be convenient to define a new related radial function like this

.

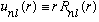So this u(r) must vanish as r->0 (since R is finite). Now, take this, plug it into the radial eqn above, and I claim (check!) that

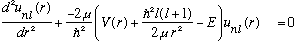
Look at this equation. It is just the usual 1 dimensional Schrodinger Eq,

only with an effective potential give by

.

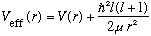This means that solving a 3-D problem with some potential V(r) is really equivalent to solving a 1-D problem with some slightly modified V(effective), and also with V(0) = infinity, or at least, we have to force u(0)=0. (Like our quiz of the "half harmonic oscillator).

And, of course, the angular part is already solved, it's just the universal Ylm's! So 3-D problems aren't really much harder than 1-D ones after all.

Example 1: Suppose we have a finite square well in 3-D. This means that if you are closer than some distance, "a", from the origin, you feel a negative (binding) potential of -V0. But, if you're further than "a" from the origin, you don't feel anything. (This is basically like the strong nuclear potential model of Gamow which we used to describe alpha decay, except without the Coulomb part, so it's for neutrons). Then, the effective 3-D problem separates into an angular and a radial piece, and the radial piece requires that we solve for the bound states of a particle in a potential which is the sum of the finite box, and the 1/r^2 "centrifugal" term...

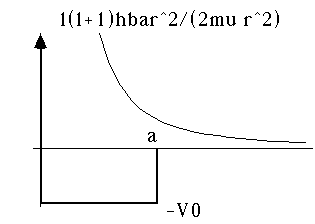which together gives

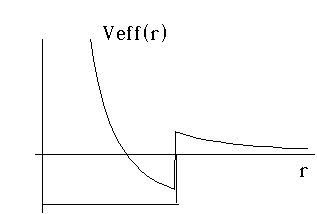
You can see that this potential could trap some particles as long as l is not too large.

For l=0, the potential is exactly the same as our 1-D finite well (only with an infinite wall at r=0) For l different from 0, the sketch is easy, and the solution is mathematically a bit more painful. We'll deal with it shortly!

Let's look at a slightly more tractable problem

Example 2: Particle trapped in an infinite 3-D well.

(So, V(r)=0 for r<a, but is infinite for r>a)

This is a lot like the example with which we started the chapter, except that the well is spherical rather than cubical in shape.

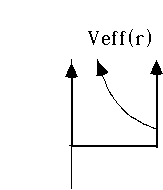
Clearly, we must have u(r)=0 for r>a (because we must have our wave function vanish out there)

And inside r<=a, the particle is free. (And again, u(0)=0)

So we are trying to solve

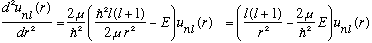
subject to u(0)=u(a)=0. Let's define (as usual)

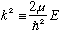
The case l =0 is especially easy to solve:

u''(r)=-k^2 u(r) => u(r) = A sin(kr) + B cos(kr)

u(0)=0 => B=0.

u(a)=0 => k = n Pi/a, and thus we find

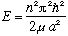, and u(r) = A sin(n Pi r/a).

Normalization says

.

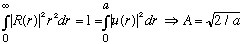Finally, what is the angular wave function, when l=0? There is only one:

.

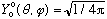Putting it all together, we get the complete wave functions when l =0:

.

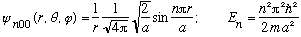The cases when l is not zero are probably not so familiar, we'll cover them next time.

Here is the Next lecture