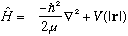
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 33 (Mon, Nov 10, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Suppose we have a system with

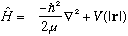
What happens to the energy of our particle, if we rotate by some angle theta about the z axis? This rotation is given by

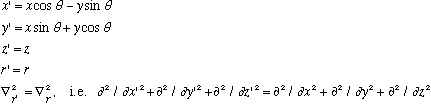
Which means

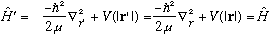
Our Hamiltonian (and thus energy) is unchanged under this rotation.

But, the wave function u(r) certainly does change: u(r') differs from u(r).

Let the rotation be infinitesimal, and let's look and see what u(r') is:

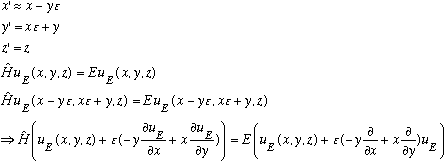
Subtracting the "old" equation from the rotated one gives

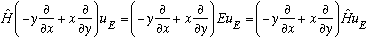
I'm going to define a new operator as follows

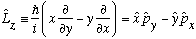
What I just showed above is that

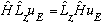
This alone does not prove the H and L_z commute, since u_E is just one specific function. But since this equation is equally true for all the u_E's, and the set of u_E's is complete, then the above equation would be true for any function at all, and thus indeed

.

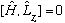Remember, this means that L_z is a constant of motion! It arose because H was symmetric under rotations about the z axis.

A symmetry of nature always leads to a constant of motion, i.e. a conservation law.

Note that

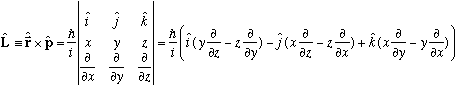
(We used the last term of this already.)

It should be clear from the spherical symmetry of our potential that there's nothing special about the z direction. I could have picked any of the axes to rotate about, and the result above would be the same, so indeed

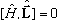
This is the quantum version of what we discussed classically above. Central forces (i.e. a potential that depends only on |r|) gives you conservation of angular momentum.

But what does this have to do with our separation of variables? Let's continue examining this L operator...

Since 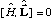, you might think (from our discussion at the end of Ch. 7) that we could simultaneously find eigenfunctions of H, Lx, Ly, and Lz. But you cannot! Why not? Because simultaneous eigenfunctions of a bunch of operators require that all those operators commute with each other!

Consider e.g.

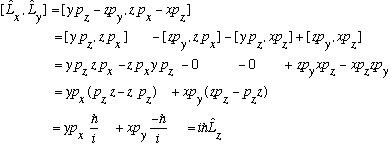
Similarly, you can show

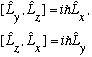
In other words, .

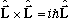This is strange! Classically, anything crossed with itself is zero, but it's not true if you can't commute operators inside. In particular, this means (again, from Ch. 7) that in general you cannot simultaneously have a complete set of common eigenstates for L_x and L_y. These two operators do not commute. They are incompatible. There is an uncertainty relation for them.

So, you can only pick one component of L to be a commuting operator with H. It's pure convention that we usually choose the z component as the "special one". It isn't really special, and you could choose x or y if you wanted. But what we've just shown is you cannot choose more than one!

Another important observation:

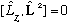. (Can you see how to prove this?)

Since we already showed 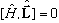, and thus

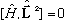(can you show this? It's not so hard) then

we can simultaneously have eigenfunctions of H, L^2, and L_z.

So our eigenfunctions u(r) will have 3 labels, specifying the (simultaneous) eigenvalue of H, L^2, and L_z.

If you work out 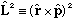keeping the order of operators straight (since some pieces don't commute) you get (see Gas for the ugly details!) .

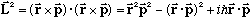It differs slightly from the classical result. The last term comes from commutators of r and p.

Solving for p^2 gives

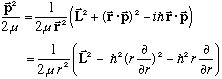
where I make use of "grad" in spherical coordinates (see the formula, given explicitly below.) You can now stick the above in the Schrod Eqn :

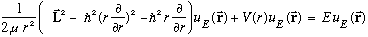
The separation of variables we got before (without really understanding what was happening?) arises because the only dependence on theta and phi in this equation comes from the L^2 term. Everything else is purely a function of r alone.

If you want to explicitly see the angular dependence of L, that's not so hard if you look up the gradient in spherical coordinates:

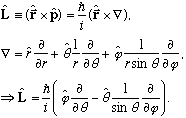
L is manifestly dependent only on the angular variables.

When you separate variables, starting from the above form, you let

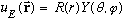, plug it in, divide both sides by u/r^2, and then argue that one piece of your equation depends only on r, another piece only on the angular variables, so each must be a constant, i.e.

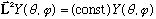
(The other equation is our old radial equation.)

The units of L^2 are certainly the same as hbar^2, so we can name this .

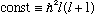Our Ylm's (which we basically worked out earlier by "brute force") are apparently eigenfunctions of L^2. By our discussion above, they are also eigenfunctions of L_z, simultaneously. We'll have much more to say about this in Ch. 11.

Here is the Next lecture