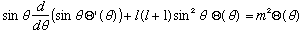
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 32 (Fri, Nov 7, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

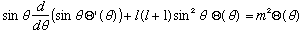
This is a second order ordinary diff eq, and the sol'ns are in Boas. They are called associated Legendre Functions,

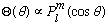
There should be two independent solutions, and there is another one. But, the other solution turns out always to blow up at theta=0 (and/or pi), which is unphysical, so we throw it away here.

Also, If |m|>l, it turns out that you cannot solve this differential equation and get a solution which is well behaved. So |m| <= l.

If m=0, the equation is called "Legendre's eq'n", and the solutions are then just the Legendre Polynomials. We'll see more details in Ch. 11, but for now let me just tell you a couple:

.

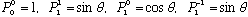The 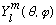fn we defined before is just the product of .

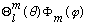The normalization convention is as follows. We would certainly like

.

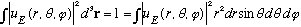To ensure this, we choose to normalize R and Y in the following way

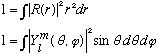
With this convention, you can easily show that e.g.

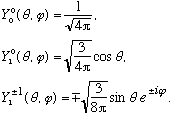
(The signs on these are pure convention, and some books differ. Beware!)

We won't purse the properties of the 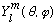's further just now. (We'll come back to them in Ch. 11.) Suffice it to say they're orthogonal (not yet obvious, perhaps, but it will be!) i.e.

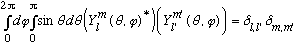
Now, go back to our original separation of the S.E, and look at the one remaining equation, the radial one. It looks like

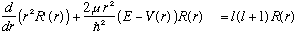
It's a second order ordinary diff eq. It does not depend on the "m" quantum # at all. It does depend on V(r). Note that 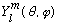did not care about V(r) at all, except for the very starting assumption that V(r) was central.

We will get back to this radial equation. It depends on the potential, and we will solve it for the case of square wells, the Coulomb potential, and others. But first, we should look more at the angular solutions, the Ylm's. We will see more clearly why the separation of variables trick worked so easily, and understand much better the significance of the Ylm functions. We will pursue this more seriously in Ch. 11, but for now, we must think about

Consequences of rotational invariance.

Our V(r)=V(|r|) doesn't care about the angles theta or phi. This turns out to be the key to understanding the Ylm's, and the lovely separation of radial and angular dependence in our equations.

Classical argument for conservation of angular momentum:

Angular momentum L=r x p, which means

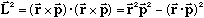
(Prove it by writing out components, or more easily with some simple geometrical arguments.) Solving for p^2 gives

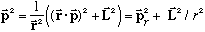
If V=V(|r|) then force (gradient of potential) is purely radial, so there can be no torque about the origin, which means L is constant in time.

Also, K.E. = p^2/2mu depends (from the above equation) only on |r| and p_r, and V(r) depends only on |r|, so the Hamiltonian, or total energy, depends only on the radial variable. Theta and phi simply don't enter. Thus, classically, you expect the energy to have nothing explicitly to do with theta and phi (beyond knowing the constant value of total angular momentum.) And vice versa, angular properties really don't care about V(r) or E.

We saw this coming out naturally when we tried separation of variables in our quantum approach. (The angular equation separated cleanly from the radial, and other than needing to know the total angular momentum, the energy was otherwise independent of the details of the angular motion.) We will see how it arises more formally, and in the process show conservation of angular momentum.

Here is the Next lecture