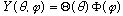Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 31 (Wed, Nov 5, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Last time, we separated r from the angular variables, and came up with an ODE for R(r), and a PDE for Y. Unfortunately, this second equation involving Y is still a partial differential equation. So, we can try separating variables again, by assuming (hoping)

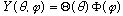. Again, plug this into the second equation we had above, divide both sides by Y, and (new trick) multiply through by sin^2(theta):

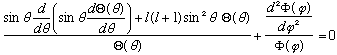
The first term depends only on theta, the second only on phi, so they must each just be a constant. I again need to come up with a name for the first constant (the second one will be just the negative of that) and I choose m^2.

Again, it's a slightly screwy name - it looks like I think this constant must be positive. Well - that's true! Let's see why. Look at the phi equation:

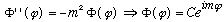
(thia solution could also have -im instead of +im, but I'll let the m's be negative as well as positive, to take care of that.)

If the constant I had chosen above had had the opposite sign, then this equation would have given me real exponentials instead of imaginary ones. But that's bad, because this function must be periodic! (Think of the physical significance of the angular variables - when you run through 2 pi, you're back at the same physical place you started.)

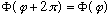
So not only must we have 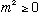but also m must be an integer.

(To get technical, this isn't completely true. Who says the wave function can't have a different phase when you run through 2 pi? That's a very weird idea, and we won't address it further this semester. But next semester we'll discover that m= (integer/2) will also give valid, sensible wave functions. But for now, we'll stick with integers. Soon (Ch. 11) we'll re-solve this whole problem via operator methods, kind of like how we re-solved the harmonic oscillator, and we'll discuss whether m must be an integer again...)

Here is the Next lecture