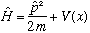Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 30 (Mon, Nov 3, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Schrodinger Eqn in 3-D: Separation in Cartesian coordinates.

The generalization of Schrodinger's equation to 3-D is about as straightforward as you could hope for. Instead of

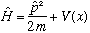(which we used in 1-D problems) we will now use

.

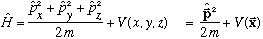As we've (briefly) mentioned before, the generalization of the momentum operator to 3-D is also straightforward,

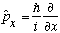, (same for y and z), or more generally .

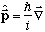Schrodinger's time dependent equation is the same as always,

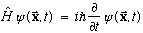. As usual, we can separate out the time dependence:

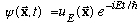, with u(x) satisfying the time independent S.E.

.

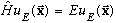(These 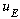's are the solutions with definite energy, and any other solution can be found by summing these up, as in Gas. 4-32.)

In real life, it is rare in 3-D problems to use x, y, and z coordinates. More often, physical systems have spherical symmetry of some kind, in which case you'd rather use spherical coordinates. But there are a few applications where x, y, and z are o.k.- e.g. huge macroscopic systems like stars where microscopic symmetry isn't so important. We will do one quick example in x, y, and z, and then put our attention to the spherical coordinate problem.

Example: Free particles in a rectangular box.

This is like the 1-D infinite well, except now there are walls in all 3 dimensions. It's a particle trapped inside a box, with infinitely hard walls, but it's free inside. (It's the 3-D version of a billiard table.) Our Schrodinger Eqn looks like this:

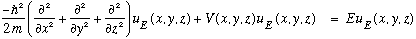
Where V is zero inside the box, and infinite outside. Let's make the box be cubical, with sides L. This partial differential equation can be solved by the (usual) technique of separation of variables: guess u(x,y,z) = X(x) Y(y) Z(z).

Take this guess, plug it back in the equation, divide everything on both sides by u(x,y,z) and notice that you end up with a sum of terms which individually depend on only one of the variables x, y, or z. (Try it yourself!)

This technique will only work if V(x,y,z) = V1(x) + V2(y) + V3(z), which is true in this case ( 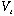is just 0 or infinity), but is not true in many other problems! But here it means that each of the terms must individually be a constant, which we give the suggestive name E:

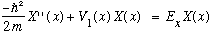
and so on for y and z. The V1(x) is 0 for 0<x<L, (infinite elsewhere),

and the total energy of the system must be

.

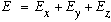This O.D.E. is exactly the same as it always was! So we know the solution:

,

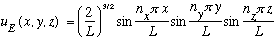and the total energy of the system is given by

.

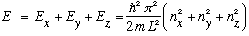We have found the allowed energies, and the corresponding eigenfunctions. I.e. we've solved everything there is to solve about this problem!

Notice that there is a lot of degeneracy in these solutions. There are often many distinct triples of integers, {nx, ny, nz} whose squares add up to the same total. E.g. {1,1,2} and {1,2,1} and {2,1,1} are completely distinct, orthogonal solutions that have the same energy. When we talk about putting more than one particle into a system, we will learn that certain particles in nature (called fermions) like e.g. electrons will not go into the same exact quantum state. So, if you start piling electrons into a box, the first can go down into the lowest state, {1,1,1} (actually 2 can be in this state, because of spin - but never mind that just yet!) The next electron has to go into one of the (3 degenerate) excited states (listed just above). And so on. This has very important astrophysical consequences - see Gas Ch. 9 for more details!

Gas. Ch. 10 - Schrodinger equation in spherical coordinates.

For most systems, spherical coordinates are much more natural than rectangular. This is because V(x,y,z) = V1(x)+V2(y)+V3(z) is very uncommon, but V(r,theta,phi)=V(r) is very common! (Potentials that depend only on distance to the origin, i.e. central potentials.) When you have a pair of particles interacting with each other by a force that depends only on distance (like electrical, or gravitational, or spring forces, etc.) it will turn out that this two particle system is completely equivalent to one particle sitting in a central potential. You must have seen this demonstrated in classical mechanics. All you have to do is use the reduced mass,

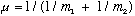, and your radial coordinate r will refer to the distance between the two particles. (Of course, there will also be a second coordinate in this case, the center of mass position. But in most cases, the center of mass will be free, and so is not especially interesting). We will work out the details of this separation when we talk about multiparticle systems.

The bottom line is that once we have solved the Schrodinger equation for a single particle in a central potential, we have also instantly solved the problem of a pair of particles interacting with a potential that depends only on distance. (which is a lot of problems, including the hydrogen atom, but many others as well). In 3-D, our Schrodinger equation for a central V is:

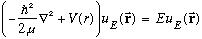
Note that by our assumption, V depends only on r = the magnitude of r.

(If we have a two particle system, mu will be the reduced mass, and the total energy will be the E from this equation plus the center of mass energy, which is P^2/2M(total), where P is the momentum of the center of mass.)

We need to remember the Laplacian operator in 3-D. Look it up in Boas, or Griffith's E+M book (or work it out!). It's ugly, but that's life:

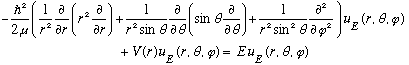
This is a 2nd order partial diff eq in 3 variables. As always, we try separation of variables, in this case let us begin by just separating out r from the other two:

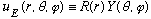
Take this, plug it into our Schrod. Eq, divide both sides by u, and (a new trick!) multiply both sides by 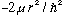, yielding

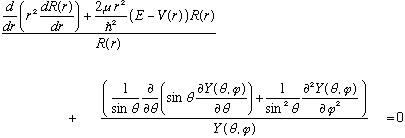
The first term is only a function of r, while the second term has no r's in it at all. This is impossible (!!) unless each term is individually just a constant, since r and theta and phi are independent variables. We have to give these constants a name (but their sum is zero, so let's only name the first one, the "r" one. The second will then just be the negative of this) and we'll call it l(l+1). That's a very odd name! If l is complex, then I claim the expression l(l+1) is in fact any constant in the world. So, it's a perfectly valid name.

(It will turn out later that this screwy form is convenient, because we will find that l must be an integer! But for now, it's just a name...)

Unfortunately, the second equation involving Y is still a partial differential equation. Next time, we will see how to solve it.

Here is the Next lecture