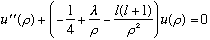Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 40 (Wed, Nov 26, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Gas. Ch. 12 - The Hydrogen Atom

Our radial equation, in unitless variables, is

,

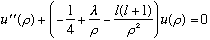a unitless, second order ODE. We can proceed like we did for the HO:

Consider first the large rho limit. This equation becomes simple:

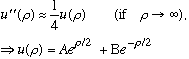
(The first term is a disaster, so we require A=0. )

We have now extracted the approximate large rho dependence, .

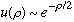As rho -> 0, our equation becomes

.

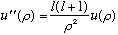It turns out this is a slightly unfamiliar but very easy ODE to solve, and the general solution is just

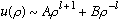
(Check! Since it has two constants, and two linearly independent terms, we've found the most general solution!) However, the "B" term is no good for small rho, as it blows up (even when l=0, it's still no good, since we require u(0)=0). Thus, we know the asymptotic behavior, and we pull it out:

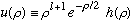
The function h is still unknown, the above equation defines it. By pulling out the asymptotic behavior, we hope that h will be a much simpler fn then u!

Indeed, we will require that h had better not diverge exponentially at large rho, and it had better have a nice power series expansion at small rho, beginning with a constant term. (Otherwise, we would not have properly pulled out the correct asymptotic behavior!) :

Now, what follows is a little painful. (The bottom line is all that really matters, but here are some details anyway...)

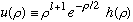. We will need two derivatives of this expression:

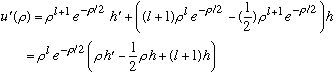
and

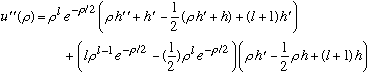
Plugging these into our radial equation yields

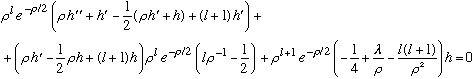
or, canceling out an overall factor of (rho^l) Exp(-rho/2),

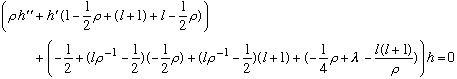
Simplifying and canceling,

.

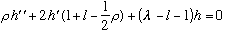This is our new version of the radial equation. Once we find h, we will then immediately know u, and R. From our discussion on the last page, we know

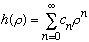
with c_0 nonzero, by construction.

We find immediately:

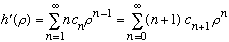
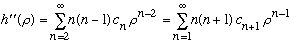
(I can make that last sum start at n=0, the "n" inside will kill the extra term)

Plugging all of this into the diff eq gives

.

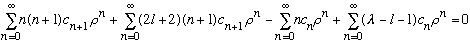Our "recursion relation" reads

.

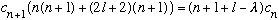Remember, we insisted that c_0 is nonzero (it will be our one overall normalization constant), and our formula then gives us all the rest of the c's! In a certain sense, we're done. We have the power series for h, as desired.

But you have to be a bit careful with power series solutions. In particular, remember our insistence that h not have nasty asymptotic behavior at large rho! Look at what happens for large n: our recursion relation looks like

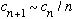, which is precisely the recursion relation for .

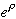This is just exactly the behaviour which we said it could not have. (It's a disaster, because now for large rho the series is blowing up.)

The only way to prevent this disaster is for the series to be finite, rather than infinite. Let's call the maximum n for the series "n_r". The only way to ensure the series ends, given our recursion formula, is if .

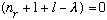But this means that

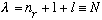is an integer. (Since n_r, 1, and l are all integers)

Since lambda tells us the energy, we have just quantized energy!

Apparently N >= l+1

(since n_r must be a nonnegative integer - remember, n_r represents the highest power of rho in the power series.)

Remembering our old result (definition) from p. 12-2:

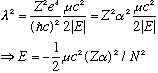
Which is precisely the Bohr formula (!!) Amazing!

Our result took quite a bit more work than Bohr, but of course there's a lot more to it.

Here are some other immediate definitions and observations:

.

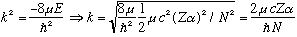I can then define a constant with units of length (previously called the Bohr radius):

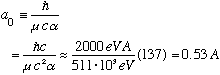
Using the above, our asymptotic radial dependence is

.

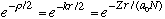A wave function with such an exponential cutoff has, by inspection, a characteristic size of roughly a_0 N/Z. (The Bohr radius is the typical size!)

Also, the numerical energy of our system (just as before) is

.

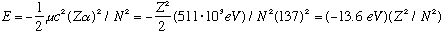Here is the Next lecture