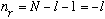
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 41 (Mon, Dec 1, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

i) Suppose N=1. Then

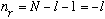
But we argued that n_r must be nonnegative, so l can only be 0 in this case.

ii) Suppose N=2. Then, .

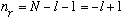Again, n_r >=0, which means there are only two possibilities:

Either l=0, and n_r = 1,

or l=1, and n_r = 0.

You can easily generalize the pattern. Given N (and thus energy)

you can have l=0,1,2,...,N-1. There are various different values of l that all have the same (degenerate) energy.

Since n_r =N - l - 1, for each different value of l (given N), you get a different n_r, which means a different polynomial for h(rho). Remember, the order of this polynomial is n_r. (And, with our recursion relation, once I tell you N, it's easy to compute h(rho)). The point is these degenerate energy eigenfunctions have completely different radial wavefunctions.

This degeneracy is a bit curious. Remember, for a particle in a 3-D spherical box, each different value of l had its own spectrum (arising from the unique zeros of the lth Bessel fn). (See Gas. p. 180) There was no connection between energies for different l's. We'll address this further, soon.

Examples: From a few pages back, we had found 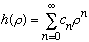, with

.

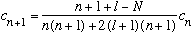Let's look at a few specific cases with N not too large. In all cases,

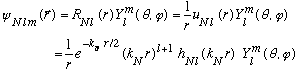
A little imposing, but still under control!

N=1:

l = n_r=0 : (the only possibility for l, as we discussed above.)

Since l=0, we have

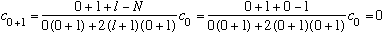
as it must be (we advertised that n_r tells the max power of rho, =0 here!)

In this case we find .

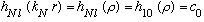This is the simplest case, and the full wave function is

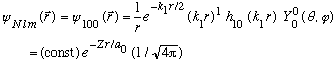
The constant can be found by normalizing. Here, it is .

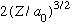N=2: (There are, as discussed above, 2 possible subcases)

Subcase a: l = 0, n_r=1 :

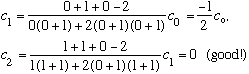
(n_r=1, so the series must stop after c_1. It's good the formula gives this!)

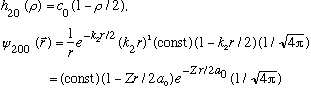
Subcase b: l = 1, n_r=0 :

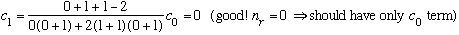
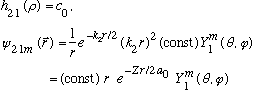
There are 3 possible m values , all with the same radial wavefunction, and the same energy. This level is 3 fold degenerate.

The total degeneracy for N=2 is 1 + 3 = 4 fold. (note 4=2^2)

N=3: (There are, as discussed above, 3 possible subcases, l=0, 1, or 2.)

Subcase a: l = 0, n_r=2 :

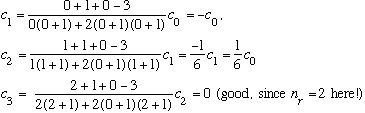
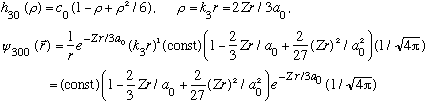
(Notice the radial function is quadratic, and it has 2 nodes.

Subcase b: l = 1, n_r=1

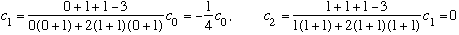
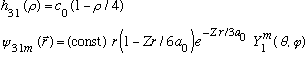
(3 fold degenerate again.) (Notice this one has only 1 node.)

Subcase c: l = 2, n_r=0

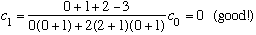
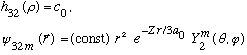
There are 5 values of m which all yield identical radial wavefns, and energy.

(There are no nodes in the radial wavefunction)

That's it for N=3. The total degeneracy is 1 + 3 + 5 = 9 (note 9=3^2)

It is a general rule that E_N is N^2 degenerate.

The notation used in the literature is as follows:

,

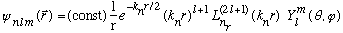with

.

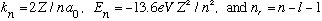The 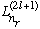is called the associated Laguerre polynomials, with order n_r, and we have seen how to generate them. (Or, you can look them up!) They are basically the same as our 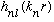functions.

It's not so hard to prove orthogonality (these are still eigenfunctions of 3 different Hermitian operators):

.

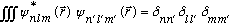More comments:

For any given N, there are a variety of allowed values for l. Can you see that the maximum l for a given N is (l=N-1)? In this case, we find

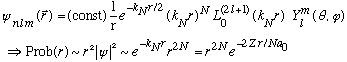
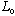( is just a constant, since it's a polynomial of order 0)

Using this, the position of maximum probability can be found by differentiating:

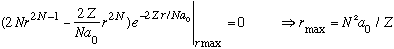
We have reproduced Bohr's formula for the radius of the Nth level. Notice that unlike Bohr's picture, r is not fixed at this value. (r is not quantized!) Also, for a given N, there are different l's besides the maximum one, and for other values of l, you will not get this same value!! Smaller l 's have nodes and bumps. Such orbits are elliptical. (Max l is as circular as you can get.)

Another nifty calculation is to look at <r>, rather than the maximum likely r (which is what we just found.)

.

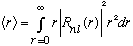This integral requires a bit of work (and now you need to normalize your wavefunction!) but you can show that it gives

.

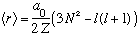Again, in the case for lmax=N-1, we get

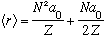
There's a (possibly surprising) extra term on the right. <r> is not the same as the most probable r, it's bigger! That's because hydrogen wavefunctions have a lot of "tail" at large r, which doesn't affect the location of the peak, but does shift the average r to larger values.

Interestingly, if you compute <1/r>, you find

,

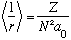the inverse of the Bohr result, and independent of l. (This result can be obtained from the Virial theorem, rather than integrating, if you like. Do you remember how that works?)

Here is the Next lecture