Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 42 (Wed, Dec 1, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

We begin with states where l=0.

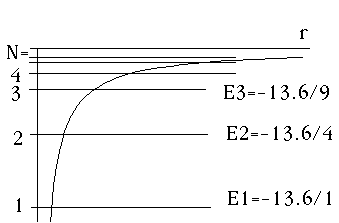
This means the effective potential in the radial equation is simply Ze^2/r. It's exactly what we originally imagined the Coulomb potential should look like. Notice that l=0 states occur for every different value of energy, or N. Look back at the above examples, and you'll see that when N=1, n_r=0, and in general for any N, n_r = N-1. So, the radial wave function goes up to terms of order r^(N-1).

l=0 => m=0. These levels, (as shown) have no degeneracy.

N.B. for these levels, R(0) is not zero.

For N=1, R(r) has no nodes (Ex 1 above)

For N=2, R(r) has one node (Ex 2 above)

For N=3, R(r) has two nodes (Ex 3 above)

It's all very much like a 1-D problem!

Next, consider the case when l=1. Now, .

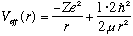Since N=l+1+n_r, and n_r >=0, we see that N=1 is impossible!

N=2 is the lowest allowed possibility. It will have n_r=0.

After this, N=3 is o.k, with n_r=1, and so on....

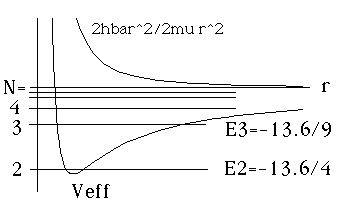
All of these levels are 3 fold degenerate

(because m = -1,0, and 1 are possible.)

R(r) for these states go like r^(l+1)/r = r

for small r: R(r) vanishes at r=0.

For N=2, R(r) has no nodes (Ex. 2 above)

For N=3, R(r) has one node (Ex. 3 above)

etc.

The real magic here is that the energies are exactly the same as the ones with corresponding N, in the l=0 plot. l is different, the radial wavefns differ, and in principle the spectrum could be totally different, but these energies overlap exactly the ones on the previous figure. This pattern continues. As l increases, you chop out the lowest energy, but from N=l+1 on, you match up!

Remember our infinite spherical box problem. We had the energy going like the square of the nth zeros of the l'th Bessel, 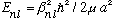. The level ordering (see notes from Ch. 9/10, Gas. p. 180) was E10 ("1s"), then E11("1p"), then E12("1D"), then E20("2s"), and so on. For hydrogen, we have N=1, (s) then N=2, (s and p degenerate), then N=3, (s, p, and d degenerate), etc. The notation is a little confusing because our conventions for n and N are different. If we labeled the hydrogen spectrum like we had labeled the box, where we counted up starting with 1 as the lowest state for each value of l , then our equivalent of n would be n_r+1, and the levels would look like the following:

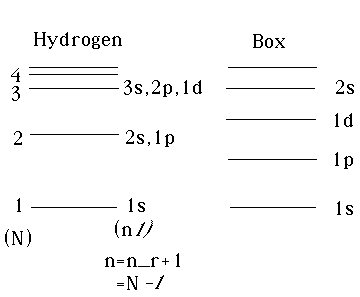
The spectra are quite different. Indeed, the energies of hydrogen are all negative, while those in the box are all positive. They're next to each just to show the ordering.

The conventional notation for hydrogen is NOT to use (n, l) as I did in this diagram, but rather to use (N,l), so we usually call them

1s, (2s,2p), (3s,3p,3d), etc...

More comments:

As mentioned along with the above figures, the Laguerre polynomial of order n_r has n_r nodes. Thus, the (Nl m) wavefunction has n_r=N-l-1 nodes, or N-l bumps.

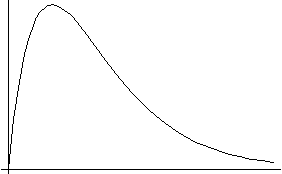
When l is as big as allowed for any given N (l=N-1 is the maximum l for any N), you always get a wavefunction with no nodes, or only one bump.

In a certain sense, this is a "ground state". See the discussion next to the figures above: if l is maximum for any given N, you can turn it around and say that given l, this case represents the minimum N. So it's the lowest allowed energy level for the given l, and has no nodes.

Gasiorowicz, pp. 210 and 210 has some nice pictures of these wavefunctions, and the next page (211) has a crude attempt at trying to picture the angular distributions. For more such nifty pictures, you might want to look at Beiser's book on modern physics, or Liboff (Ch. 10), or just about any other quantum text. Curiously, Griffith's book doesn't have particularly enlightening plots...

We have solved the hydrogen atom in pretty gory detail! By using reduced mass instead of m_e, you get the energies correct to better than 1%. There are some small and subtle corrections to our story, mostly involving spin (and relativity), some of which we will come back to in QII. But now we return to the one topic we missed in Gasiorowicz (Ch. 8) which deals with the situation where more than one particle is present in your potential...

1 particle                  N particles

Wave function: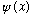                                   
Prob(particle at x) =    Prob(part. #1 is at ,#2 is at ,..., 
                             (etc.), #N is at )   =            
Norm:                                            
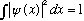
Expectation value of operator: 
                                             
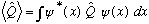
Schrod Eq:                                     
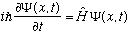
Hamiltonian:                                    
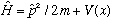
Commutation relations:        
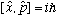
	        (because different particles are independent)                 
Def. of momentum:                                 

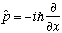
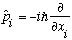
Here is the Next lecture