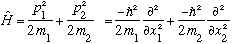
Physics 3220, Fall '97. Steve Pollock.

3220 - Notes, lecture 44 (Mon, Dec 8, 1997)

Here is the previous lecture

Here is the Next lecture

Back to the list of lectures

Suppose first there was no potential at all, so we are simply describing 2 non-interacting free particles. We can write down the Hamiltonian:

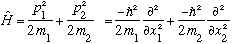
and, as usual, we are trying to solve Schrodinger's Eq, which here looks like

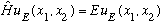
This is a PDE in two variables, x1 and x2. So, try separating variables!

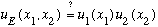
(Perhaps this even makes some physical sense. I would expect the probabilities to factorize: Prob(x1,x2)=Prob(x1)Prob(x2). It's sort of like arguing that the probability of getting "snake eyes" is (1/6)*(1/6) = 1/36. The two dice are independent, so the total probability of some joint outcome is the product of the individual probabilities. )

Anyway, we try plugging this product solution into our Schrod. Eq:

.

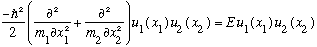Expand out the sum, and divide both sides through by u_E, to get

.

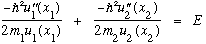We have a sum of two terms equaling a constant. But each term is a function of an independent coordinate, so this is impossible! It's the usual separation of variables trick. The only way this equation can make sense is if each of the two terms on the LHS is separately a constant. Give them names, e.g. E1 and E2. Then we have two distinct ODE's that are easy enough to solve by inspection:

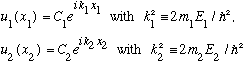
Putting it back together, we have found

.

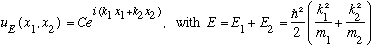This is indeed the answer, but we can make it look perhaps a little more sensible by switching to a new set of variables:

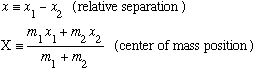
You can (should) check for yourself that I can invert these equations:

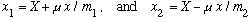
where I have introduced the reduced mass

.

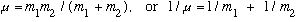You can also check that .

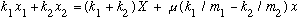Because of this relation, I will also define new momentum variables:

.

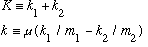Again, you can (should) check for yourself that I can invert these:

.

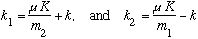With all of these new definitions, I can rewrite my wavefunction in terms of x and X, and k and K:

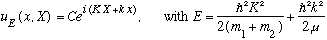
(You'll have to check that the energy expression is correct, the wave function is pretty direct.)

This separation has a rather nice physical interpretation.

The 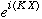part looks like a plane wave for the center of mass, moving with total momentum K. The 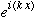left over must be some kind of "internal wave function", since it involves relative position and momenta, although here it is still a plane wave. (Since in this example there was no potential at all, the particles are totally free.) Also, the total energy makes total sense! The first term looks like the kinetic energy of the center of mass (traveling with total momentum K, and total mass m1+m2), and the second term would be some kind of "internal" or relative kinetic energy, using a reduced mass.

This change of variables we've set up is especially useful whenever the potential depends only on the relative separation ("2 body potential"), 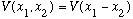. To see why, we need to do a little algebra to rewrite our Schrodinger Eq in the new variables x and X:

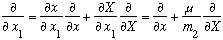
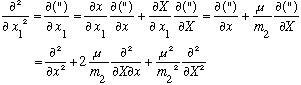
(You should verify this if you don't see it). Similarly, we find

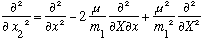
Putting these last two expressions into our Hamiltonian, we can convert to (x,X) space instead of (x1, x2):

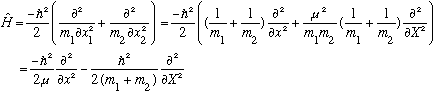
The cross terms have canceled, and what we're left with makes reasonable sense. The kinetic energy in the Hamiltonian has two pieces, the first represents the "internal" or relative kinetic energy, the second is the kinetic energy of the CM.

If there is no potential, then solving

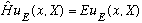is done instantly and easily by separation of variables, and you get precisely what we had above, by inspection:

.

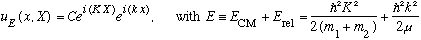But now, including a potential of the form ,

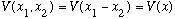our Schrod equation becomes

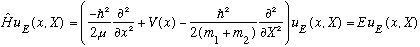
This can still be solved by separating variables (x, and X), giving

,

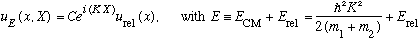where

.

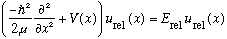This last equation is our regular old Schrod equation for a single particle. This is what I meant earlier when I said that any two particle system with a potential that depends only on the separation looks effectively like a single particle in that potential, only with reduced mass.

(And, there is of course an extra additive term to the energy which can often be ignored, the kinetic energy of the free center of mass. The center of mass motion is simple, separable, it's just that 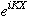plane wave business.)

Identical Particles.

I've been labeling my particles # 1 and # 2. This is a purely classical idea! It's still fine in quantum if they're distinguishable (e.g. the e and p in hydrogen) but is not o.k. if they are identical (e.g. two electrons). It's like naming twins. As they go through life, even though they may be identical, I imagine that I always somehow know which (who) is #1 and who is #2. But, in QM, we must give up this idea! When 2 electrons are identical (they all are) we cannot in any way distinguish them. So, what we've done with our labeling so far is risky, and in a real sense incorrect. The fix is to say that

H must be invariant under interchange of particles.

(If you cannot tell who is #1, and who is #2, switching them cannot affect the energy.)

Consider a 2 particle Hamiltonian like the ones we've been writing down.

.

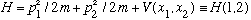The eigenfunctions of this will be .

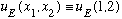These equations should perhaps be viewed as a bit more general than they appear. E describes the state, and may of course involve a set of quantum numbers like "nlm" in 3D, or something, and not necessarily just energy. Similarly, "x" may also be more than just the position (it could also be the y and z coordinates in 3-D, or the spin coordinate of the particle, etc.) That's why I dropped the x's and just used the numbers "1" and "2" above.

Let's now define a new operator, the exchange operator, 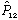. It's vaguely a bit like parity, but in this case it's the operator which swaps two identical particles we've labeled "1" and "2". Formally

.

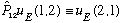Clearly, P^2 =1 (swapping twice is the same as doing nothing), so the eigenvalues must be 1 or -1. (Do you see why?)

Now, we already had written down the 2-particle Schrodinger Eqn:

.

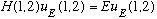In the above equation, you should be able to change labels freely (they're just dummies, I'm calling the particles 1 and 2, but could just as easily call them A and B or, for that matter 2 and 1) which means

.

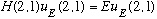But I argued that interchanging particles doesn't affect the energy, i.e.

H(1,2)=H(2,1). Plugging this into the last equation says

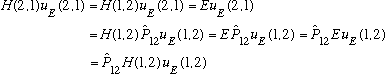
That's all a big string of equal signs. Comparing the first term in the last two lines (and making use of the fact that u_E is a complete set of 2 particle wavefunctions)

.

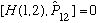P12 is a constant of motion. If you start off in an eigenstate of P12, you will stay that way forever. "Exchange parity" is conserved. This is just another example of how a symmetry of the Hamiltonian (here, exchange symmetry) leads to a conservation law. (What are the eigenstates of P12? Think about parity, it's similar: the e-states of P12 are symmetric, or antisymmetric, under interchange of particles.)

If you have some wavefunction 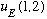which is not an eigenstate of P12, you can always quickly and easily construct such a state:

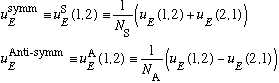
Check for yourself that these states are eigenstates of exchange, i.e.

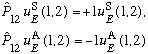
Now here's the weird part. It is apparently a law of nature that symmetry (or antisymmetry) under exchange is a characteristic of all particles. You cannot in reality chose or construct it, like you could with parity. For instance, electrons (and in general particles with half integer spin, which we call generically fermions), are always found in antisymmetric wave functions in nature! You can never find, or make, a system of two electrons in a symmetric wavefn, only antisymmetric. Pauli was the one who first stated this law of nature, and it's sometimes known as Pauli's principle.

Similarly, pions (and photons, and in general particles with integer spin, called generically bosons), are always found in a symmetric wave function in nature! Our results above tell us that, once a boson, always a boson. (conservation of exchange symmetry.)

If you have 3 (or more) identical fermions, nature must put them into a state which will be antisymmetric under interchange of any pair!

Say our Schrodinger's equation has some 3 particle wavefunction 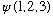that appears to satisfy all desired boundary conditions of some problem. (it need not have any particular exchange symmetry at all). If the particles are electrons, they will not ever be observed in this state 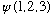, but rather in .

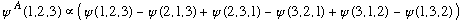If the particles are bosons, then all those minus signs must be plus signs. These new states have been "symmetrized" or "antisymmetrized" with respect to exchange of any 2 of the particles (convince yourself!)

You could, in principle, have imagined mixed states of nature. For example, you might imagine 3 identical particles such that if you swap 1 and 2, your wave function changes sign, but if you swap 2 and 3 it does not. But, such states do not appear to ever be found, or be constructable, in nature.

As a consequence, all 2-particle wavefunctions describing identical particles satisfy .

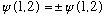The plus sign (symmetric) is for bosons. The minus sign is for fermions.

Unlike the energy, the wave function itself is not invariant under particle interchange. (It flips sign, at least for electrons).

Example: put two electrons in an infinite box, with total energy E:

,

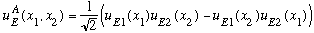with .

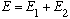(Verify for yourself that if you switch 1 <-> 2, you get exactly what you started with, only with a minus sign)

The way I might think about this wave function is that

particle #1 is in the state with energy E1, and particle #2 is in state E2

or particle #1 is in the state with energy E2, and particle #2 is in state E1, and these two occur with equal likelihoods (so I superpose them).

The particles are identical, so you cannot possibly distinguish between the above two statements. The real physical state is simply this linear superposition of the two possibilities!