Exam Info | Physics 1110

Exam Information

There will be three midterms and a final:

Exam	Date	Time	Location
Midterm 1 (See below for more info)	Thurs, Sep 24	7:30-9:10 PM	Exam locations
Midterm 2 (See below for more info)	Thurs, Oct 22	7:30-9:10 PM	SAME AS LAST TIME!
Midterm 3 (See below for more info)	Thurs, Nov 19	7:30-9:10 PM	SAME AS THE LAST TIME!
Final (See below for more info)	Wed Dec 16	10:30 AM - 1 PM	Coors Event Center, Seating is Assigned. Figure out where you are sitting, bring that info with you!

For details about course grading, please see our detailed grading page!

Exams will be cumulative, and will be all multiple choice. Calculators with scientific notation are allowed. (Of course, no phones, internet access, "electronic crib sheets", etc!) Graphing calculators are ok too, just don't use them to store stuff - that's what your crib sheet is for. You are allowed to bring a single 8.5" x 11" formula sheet to the exam. You can write anything you want on your formula sheet (both sides!) but you must write it by hand - no photocopying, typing or sharing allowed.
Calculators with scientific notation are allowed. (But, no phones, no calculators with internet access, "electronic crib sheets", etc!)

___________________________________________________________________________________________

Final Exam:

The location of the Final Exam is Coors Event Center. NEW: Seating is ASSIGNED. Bring your student ID, please.

As with all midterms, you can bring ONE 8.5x11 formula sheet to the exam, handwritten, with whatever you like on it.
The format of the final is just like the midterms. Because we have 2.5 hours, the length of the exam will be roughly 42 questions.

The final exam covers material from the entire course - Chapter 1 through 15 of Wolfson (our etext) and/or our notes. (There will NOT be questions about "temperature and heat"!)

Exams are cumulative (this is the nature of physics) which means you are still responsible for earlier material. The final exam will cover new material since the third midterm, so definitely expect to see some questions on Simple Harmonic Motion, fluids, and waves (Ch 13-15) , but also expect to see quite a lot of material from earlier in the course on the final as well!

Older material: Introduction, units/dimensions, 1-dimensional kinematics, the basic math of vectors, projectile motion, and Newton's 3 law3, applying Newton's 2nd law (including multiple objects, forces in various directions, circular motion, etc), Work and Energy (and conservation of energy), and Gravity, including orbits, gravitational energy, and escape speed.

- Center of mass, momentum, conservation of momentum, Elastic and inelastic collisions.

- Rotational motion, including kinematics, torque, moment of inertia, rotational kinetic energy, and rolling motion.

- Angular momentum, conservation of angular momentum, angular variables as vectors, including the "right hand rule" for directions. The cross product. We won't test you on "gyroscopes and precession".

- Static equilibrium (including F_net=0 and torque_net=0)

New material also on the final:

Ch 13: Simple Harmonic Motion, including mass on spring, the simple pendulum, use of energy conservation in SHM, and relation of circular motion to SHM. (Note: we did not cover 13.6 or 13.7)

Ch 15: (sections 1-3 only) Fluids: density and pressure, how pressure varies with depth, and Archmide's principle.

Ch 14: Waves, traveling waves and sinusoidal "wave math". (We will not cover section 14.8)

See the bottom of this page for more info.

We include anything covered in lecture, posted lecture notes, Tutorial activities and Tutorial homeworks and MP homeworks and prelecture videos up through the start of the week of the exam, and/or anything covered in our textbook and online notes, again up to the start of the week of the midterm. (Generally, the "material" cutoff is whatever we cover the Friday before the exam, but Monday and Wed lectures the week of the exam will also include some review and practice, plus a bit of new stuff that won't be on this test... )

There is a practice test available on D2L. Prof. Dubson also provided a content summary document. (Right now it still includes info about heat, but remember that we are cutting the final exam off at Chapter 14 and Chapter 15, nothing past that)

Other review/practice options: read the text! Also/or read our online lecture notes. Look for the Conceptual Examples scattered througout (Called "Got it" in the e-text - there are answers at the very end of each chapter!) Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Thought" questions at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say more "concept question-like" than "computational" on the whole, just like the previous exam )

Look at the "Lecture Info -> Concept Tests" tab, you will find more concept tests than we get to in class. The day before the exam we have a review class, and there again you'll find more concept tests online than we cover in class. Look at the homeworks (including Tutorials) and ask yourself "how could they take the physics ideas of this problem, change them a bit, and turn them into a multiple choice exam question"? Don't bother memorizing solutions to the homework, we're not going to ask the same questions - but we will look at the methods and ideas behind the problems and test to see if you have understood those and can apply them in a novel situation.

Check out the resources for "Wolfson: Essential University Physics" (etext) within our Mastering Physics site.

Expect to see questions you have never seen before (we do not repeat problems we've already asked you!) but they will be related to what you work on in clicker questions, Tutorials, text examples, and the homeworks. We want you to show off your conceptual and computational/problem-solving skills, we're interested in your understanding of the physics, we are not interested in memorization or plug-n-chug behaviour or rote procedures.

For specific chapter by chapter learning goals, see the bottom of this page for more info!

___________________________________________________________________________________________

Older information -

Exam #3:

Results for Exam 3:

We do NOT assign a letter grade to individual exams. There is no point in doing so, since each exam is only a fraction of your grade. (See our detailed grade page for figuring out your estimated course grade!)
Here is a histogram of the scores on Exam 3:

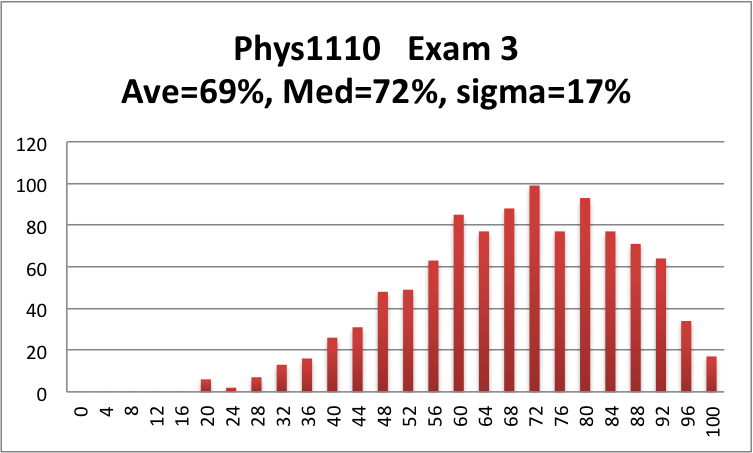
As you can see, the class overall did very well, this is once again a strong average for the third midterm in this course!
The average is 69%, and the median is 72%. (~20 students had perfect scores. If your personal score on Exam 3 is lower than you would have liked, take a look at our general advice page here (and then follow up with our "Resources -> Advice" tab above.)

What is much more relevant than your individual exam score is your total course score so far (including Mastering Physics, and Tutorial Homework and attendance) D2L keeps updates of your other course scores (MP and clicker scores get updated around exam dates) so you can work this out for yourself.
As always, for details about course grading, please see our detailed grading page!

_____________________________

Exam 3 information: Location: Go where you were assigned to go last time (unless you formally changed sections since the first midterm)

See above - you can bring ONE 8.5x11 formula sheet to the exam, handwritten, with whatever you like on it.

The third midterm covers material from the course through the week up to the exam, this is Chapter 1 up to and including all of Ch 12, and the start of Ch 13 (through section 13.2) of Wolfson (our etext) and/or our notes.
Exams are cumulative (this is the nature of physics) which means you are still responsible for earlier material - but of course exams tend to have more of a focus on new material since the previous midterm. (So look down this page, under exam 1 and 2, for more useful information about older material to review/study!)

Older material: Introduction, units/dimensions, 1-dimensional kinematics, the basic math of vectors, projectile motion, and Newton's 3 law3, applying Newton's 2nd law (including multiple objects, forces in various directions, circular motion, etc), Work and Energy (and conservation of energy), and Gravity, including orbits, gravitational energy, and escape speed.

Newer material (the focus):

Ch 9: Center of mass (we won't have you do integrals to find this, just collections of point masses), momentum, conservation of momentum, Elastic and inelastic collisions in 1-D and 2-D, and Newton's 2nd law applied to systems (F_net = m_total* a_center of mass).

Ch 10: Rotational motion, including kinematics, torque, moment of inertia, rotational kinetic energy, and rolling motion.

Ch 11: Angular momentum, conservation of angular momentum, angular variables as vectors, including the "right hand rule" for directions. The cross product. We won't test you on "gyroscopes and precession".

Ch 12: Static equilibrium (including F_net=0 and torque_net=0)

Ch 13: Just the beginnings of SHM, up through Section 13.2 in your text.

There is a practice test available on D2L. Prof. Dubson also provided a content summary document.
Other review/practice options: read the text! Also/or read our online lecture notes. Look for the Conceptual Examples scattered througout (Called "Got it" in the e-text - there are answers at the very end of each chapter!) Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Thought" questions at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say more "concept question-like" than "computational" on the whole, just like the previous exam )

Look at the "Lecture Info -> Concept Tests" tab, you will find more concept tests than we get to in class. The day before the exam we have a review class, and there again you'll find more concept tests online than we cover in class. Look at the homeworks (including Tutorials) and ask yourself "how could they take the physics ideas of this problem, change them a bit, and turn them into a multiple choice exam question"? Don't bother memorizing solutions to the homework, we're not going to ask the same questions - but we will look at the methods and ideas behind the problems and test to see if you have understood those and can apply them in a novel situation.

Check out the resources for "Wolfson: Essential University Physics" (etext) within our Mastering Physics site.

For specific chapter by chapter learning goals, see the bottom of this page for more info!

___________________________________________________________________________________________

Exam #2:

Results for Exam 2:

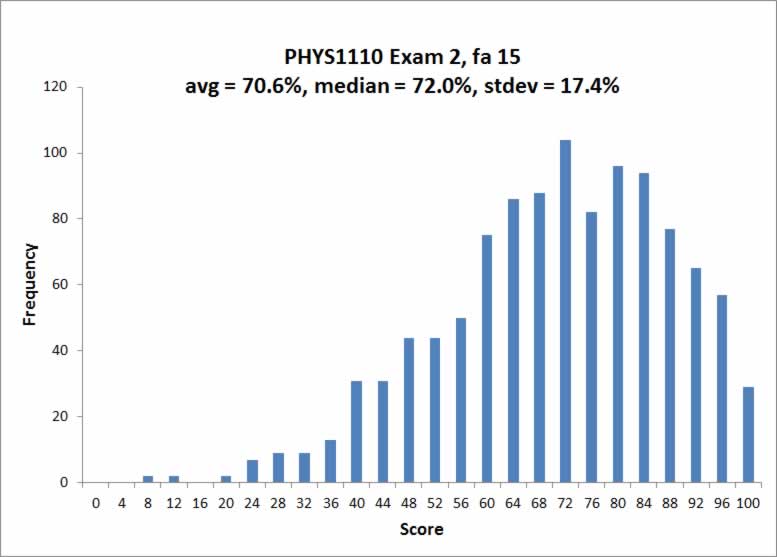
As you can see, the class overall did very well, this is historically a strong average for the second midterm in this course!
The average is 71%, and the median is 72%. (~30 students had perfect scores. About 20% of the class scored above 90%, and over half the class scored >=72%. Well done! If your personal score on Exam 2 is lower than you would have liked, take a look at our general advice page here (and then follow up with our "Resources -> Advice" tab above.

Older: Exam 2 information: Location: Go where you were assigned to go last time (unless you formally changed sections since the first midterm)

See above - you can bring ONE 8.5x11 formula sheet to the exam, handwritten, with whatever you like on it.

The second midterm covers material from the course through the week before the exam, this is Chapter 1 up to and including all of Ch 8 of Wolfson (etext) or our notes.
Exams are cumulative (this is the nature of physics) which means you are still responsible for earlier material - but of course exams tend to have more of a focus on new material since the previous midterm. (So, see below under exam 1, for more useful information about older material to review/study!)

Older material: Introduction, units/dimensions, 1-dimensional kinematics, the basic math of vectors, projectile motion, and Newton's 3 laws.

Newer material (the focus) : Applying Newton's 2nd law (including multiple objects, forces in various directions, circular motion, etc), Work and Energy (and conservation of energy), and Gravity. See the bottom of this page for more info.

We include anything covered in lecture, posted lecture notes, Tutorial activities and Tutorial homeworks and MP homeworks and prelecture videos up through the start of the week of the exam, and/or anything covered in our textbook and online notes, again up to the start of the week of the midterm. (Generally, the "material" cutoff is whatever we cover the Friday before the exam, but Monday and Wed lectures the week of the exam will also include some review and practice, plus a bit of new stuff that won't be on this test... )

There is a practice test available on D2L. Prof. Dubson also provided a content summary document.
Other review/practice options: read the text! Also/or read our online lecture notes. Look for the Conceptual Examples scattered througout (Called "Got it" in the extext - there are answers at the very end of each chapter!) Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Thought" questions at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say more "concept question-like" than "computational" on the whole, just like the previous exam )

Look at the "Lecture Info -> Concept Tests" tab, you will find more concept tests than we get to in class. The day before the exam we have a review class, and there again you'll find more concept tests online than we cover in class. Look at the homeworks (including Tutorials) and ask yourself "how could they take the physics ideas of this problem, change them a bit, and turn them into a multiple choice exam question"? Don't bother memorizing solutions to the homework, we're not going to ask the same questions - but we will look at the methods and ideas behind the problems and test to see if you have understood those and can apply them in a novel situation.

Check out the resources for "Wolfson: Essential University Physics" (etext) within our Mastering Physics site.

For specific chapter by chapter learning goals, see the bottom of this page for more info!

__________________________________________________________________________________________________

Older: Results for Exam 1:

As you can see, the class overall did very well.
The average is 75%, and the median is 80%. (Over 20% of the class scored above 90%, and over half the class scored >= 80%. Nice job!! If your personal score on Exam 1 is lower than you would have liked, take a look at our general advice page here (and then follow up with our "Resources -> Advice" tab above.

What is much more relevant than your exam 1 score is your total course score so far (including Mastering Physics, and Tutorial Homework and attendance) We'll upload MP data to D2L soon (Alas, the systems are not coupled directly) so you can see this "combined score" so far for yourself - (But until then, you will have to see how you're doing inside MP and figure it out for yourself.) If your Tutorial scores are not appearing in D2L, please check with your TA to figure out what is happening, they should be in there.

STUDY INFORMATION FOR EXAM 1:

The first midterm covers material from the course through the week before the exam, this is Chapter 1 up to and including all of Ch 4 of the etext:
Introduction, units/dimensions, 1-dimensional kinematics, the basic math of vectors, projectile motion, and Newton's 3 laws.

This includes anything covered in lecture, posted lecture notes, Tutorial activities and Tutorial homeworks and MP homeworks and prelecture videos up through the start of the week of the exam, or anything covered in our textbook and online notes, again up to the start of the week of the midterm. (Generally, the "material" cutoff is whatever we cover the Friday before the exam, but Monday and Wed lectures the week of the exam will also include some review and practice, plus a bit of new stuff that won't be on this test... )

There is a practice test available on D2L. Prof. Dubson also provided a content summary document.
Other review/practice options: read the text! Also/or our online lecture notes. Look for the Conceptual Examples scattered througout. Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Questions" at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say more "concept question-like" than "computational" on the whole) Look at the "Lecture Info -> Concept Tests" tab, you will find more concept tests than we get to in class. Look at the homeworks and ask yourself "how could they take the physics ideas of this problem, change them a bit, and turn them into a multiple choice exam question"? Don't bother memorizing solutions to the homework, we're not going to ask the same questions - but we will look at the methods and ideas behind the problems and test to see if you have understood those and can apply them in a novel situation.

Check out the resources for "Wolfson: Essential University Physics" (etext) within our Mastering Physics site.

Our course has higher-level learning goals, but in terms of content for the first exam, here are some of our more explicit chapter by chapter learning goals. Think there's something really key that's missing below? Could be!! This list is suggestive, it's not meant to be difinitive. Post your thoughts on piazza!
____________________________________________________________________________________________________
CHAPTER BY CHAPTER LEARNING GOALS

Each line below should be preceeded by You are expected to....

Ch 1: Introduction
... use the correct number of significant digits in calculations

... convert from one unit to another, even with complicated derived units like m/s^2 to inches/month^2, for instance. (Note that we do not expect you to memorize or waste crib-sheet space on constants and conversions. We will give you anything you need except perhaps the most elementary facts, like 12 inches in a foot, or 60 minutes in an hour, etc...)

... know the basic metric prefixes (specifically: milli, centi, kilo, and mega) (Any others we would likely define for you)

... be able to work with SI metric units (m, s, and kg so far), including knowing "typical numbers" (what we call the order of magnitude) of everyday physics quantities. (Like roughly how big a person is (order 1-2 metres), or how fast you walk (1-2 m/s), etc)

... be able to calculate the dimensions of physical quantities from formulas, and use this to decide if formulas are possible or impossible. (This is called "checking units". It can be a good way to eliminate obviously wrong answers!)

... be able to read and use scientific notation (powers of 10) in expressing large or small quantities, and doing basic manipulations (like multiplication or division) with it.

Ch 2: Kinematics

... know the difference between distance and displacement, and be able to compute either given a story, graph, or formula.

... choose a coordinate system, and know what changes when you "flip" the choice of positive direction.

... know the difference between speed and velocity, and be able to find either given a story, graph or formula. This includes being able to differentiate (take a derivative) of a simple formula or graph for x(t) to get v(t) = dx/dt.

... know the difference between average and instantaneous quantities, and be able to use a graph, equation, or numbers to estimate either one (e.g. given a simple x versus t graph, you should be able to compute average velocity over any time interval, and instantaneous velocity at any point)

... know the definition of acceleration and be able to extra it from stories, graphs, or formulas. This includes being able to differentiate (take a derivative) of a very simple formula or graph for v(t) to get a(t) = dv/dt.

... extract the sign of velocity and acceleration from graphical means (e.g. "seeing" how the slope of the velocity vs time graph tells you the sign of acceleration)

... be able to "tell the story" from a graph or formula, so you can describe what is physically happening.(Or vice versa, be able to go from a story to a sketch or formula)

... solve basic "word problems" involving the 4 central "constant acceleration" 1-D kinematics equations (Wolfson Section 2.4). This includes being able to choose a coordinate system (or work in one that we choose for you, which might be backwards from what you normally use!), decide which equation is the appropriate one to use in a given situation, do basic algebra to manipulate those equations, and interpret all the symbols in the equations.

... manipulate these 1D equations with numbers but also WITHOUT numbers (purely symbolically), including being able to take derivatives of very basic (power-law, like constant*t or *t^2 or *t^3, etc) functions. (We know that many of you are taking calc I for the first time now - we will NOT be "pushing" your calculus knowledge! All we want is what you have done on homework so far, nothing more yet...)

... solve simple "multi-step" 1-D kinematics problems, where e.g. the "final" velocity from one part of the problem becomes the "initial" velocity in the next part. (Graphically, this means situations which are no longer constant acceleration, but are "piecewise" constant acceleration: so that each time period has constant acceleration)

... recognize when problems involve "freefall", and thus solve constant acceleration problems involving the acceleration of gravity.

... avoid common misconceptions as described in the text and class (e.g. avoiding the misconception that acceleration and velocity must always be in the same direction, avoiding the misconception that acceleration is zero at the top of a freefall trajectory, avoiding the misconception that a = v/t rather than delta v/delta t, avoiding the misconception that if you know velocity as a function of time, then the motion must start at x=0 (it could start anywhere, unless you are explicitly told!), avoiding the misconception that g is negative (it is definited to be+9.8 m/s^2: the sign of acceleration depends on your choice of coordinate system)

... solve problems in 1D even if they are "tilted" (like objects on an air track)

... move comfortably back and forth between graphs of (x vs t) (v vs t) and (a vs t)

... intepret the above graphs to be able to describe the physics, or vice versa (e.g. sketching a graph given a description of the motion)

Chapter 3: Vectors.

... distinguish between a vector and a scalar quantity, and decide whether some given physical quantity is one or the other

... be able to compute the components of a vector given a graphical picture of the arrow, and vice-versa: find the angle and length of a vector given the two components.

... know the basic geometrical trig identities (definitions of sin, cos, and tan) and be able to work your calculator to take those functions or the "inverses" to find angles.

... add vectors graphically.

... Know and use the definition of "Delta" (the "change") so you can e.g. convert the formula V1 + Delta V = V2 into a picture, and vice-versa.

... add vectors using the method of components

... subtract vectors graphically, or using the method of components.

... multiply vectors by a scalar of either sign (graphically, or with components)

Projectile Motion.

... recognize problems which are 2-dimensional "free fall" (without being explicitly told) and be able to set up and solve the usual equations of motion in x and y-directions (which includes times, distances in x, and y, and velocities)

... use "unstated" elements of free fall problems (e.g. acceleration is -g in the y-direction if we call up "positive", but acceleration is 0 in the x-direction, the y-component of velocity is zero at the peak, etc)

... draw and/or interpret diagrams involving projectile motion, and be able to extract or solve for the x- and y-components of all vectors involved.

... Find differences of vectors either graphically or through components, and thus e.g. relate initial and final position vectors to Delta x, and relating that to average velocity, all in 2-D (and similarly for velocities/average acceleration)

... distinguish between speed (a non-negative scalar) and velocity (which is a vector) in 2-D problems

... know when the formula a = v^2/R (centripetal acceleration) is applicable (uniform circular motion, steady speed), and apply it.

... be able to identify and explain the direction of acceleration vectors for arbitrary 2-D motion (like in the Tutorial where objects move on funny-shaped tracks with possibly changing speed!!)

Newton's Laws. (Ch 5 and 6)

... Identify and properly label forces.

... draw a proper free-body diagram, labeling forces: force ON object BY another object, and identifying what kind of force (e.g. tension, gravity, normal, friction)
... apply Newton's second law in a wide variety of problems. This includes using a free-body diagram to generate an equation (in 2D, that means one equation for x-,another one for y-) and use it to solve for acceleration. Alternatively, if the acceleration is known (given, or implied by the problem) then the equation can be used to deduce unknown forces.
... Use Newton's third law. (This means you recognize situations where it applies, you properly attribute forces to the correct object, and you get the signs of all force components correct)
... identify the "normal force" in problems, and use Newton's laws (2 and 3) to deduce the normal force in e.g. tilted tracks, or in situations with "stacked" objects

... combine multiple forces acting at different angles (using basic vector addition)

... ihandle multiple connected objects (recognizing e.g. when objects must have the same acceleration). This includes "Atwood's machine" or variants...
... solve problems with weight (mg) and "apparent weight" (normal force when you are also accelerating up or down), including "weightlessness = free fall"

... solve problems involving friction. You should know the formula for kinetic friction (f=mu_k N), and be able to deduce from the problem what the normal force is (which may itself require a free body diagram, see above.)

... solve problems involving static friction. Here, there is no formula (!!!), which you should be able to handle. Know that static friction means "no motion", so you know acceleration=0, and know that there is a formula for "maximum possible static friction = mu_s N". Recognize when you are allowed to use this formula for static friction (e.g. if the object is "just about to move") and when you can not (almost all other situations!)

... know that for any pairs of materials in contact, mu_s > mu_k.
... solve basic Newton's 2nd law problems when an object is moving with uniform circulation motion, which includes setting up a free-body diagram, writing down, and solving Newton's second law in component form.

... know when the formula a = v^2/R (centripetal acceleration) is applicable (uniform circular motion, steady speed) and use it as part of circular motion force problems.

...be able to find the speed needed for circular motion, or given the speed, find one of the unknown forces (often "normal" or "tension"). This includes recognizing limiting situations (e.g. that Normal force or tension can never be negative, which sometimes sets a limit on allowable speeds around a loop)

Chapter 6 and 7 Work and energy, and conservation of energy

... know the basic definition of work done by a given force, and be able to compute it even when the force and displacement do not "line up". This includes computing dot products (given magnitudes and angles OR components) and getting the SIGN of work correct!
... know the basic definition of kinetic energy, and thus be able to compute KE, and changes in KE.
... distinguish between "net work" and "work done by a particular force"

... deal with problems where force is not constant, or path is not straight line, by adding up "chunks" of work. (We will not expect you to be able to compute integrals yet, but you should know the idea of the integral as "area under the curve", and be able to use that e.g. to find work done if presented with a graph of force vs position.
... know and propery use metric units for work and energy (the definition of the Joule)
... use the work-energy principle to relate net work done and the change in kinetic energy of an object
... know the formulas for potential energy (PE) arising from gravity near the surface of the earth (mgy) and also from an object on an ideal spring (1/2 k x^2)

... know that (change in) PE is defined as the negative of the work done by a conservative force (and why that negative sign is needed)
... know and use Hooke's law (F = -kx) in problems involving masses connected to springs, including interpreting the sign in Hooke's law correctly)
... use the principle of conservation of energy to solve basic problems in 1- and 2-d involving objects where energy changes form (from kinetic to various forms of potential energy) This includes recognizing problems where mechanical energy is or is not conserved (e.g. when frictional forces are present, or external forces)
... solve basic problems where friction or external forces are involved, still using the principle of conservation of energy, but now including the "W_friction + W_external" term to relate initial energy to final energy of a given system. (This will require knowing the sign of those extra work terms)

... be able to interpret "energy graphs" (called "potential energy curves" in the text), and use them to determine KE and PE at different positions, identify turning points and qualitatively describe motion.
... know the basic definition of power (change in energy/change in time), and the alternative form (force_parallel times speed) to be able to compute or compare powers

Gravity (Ch 8)

... use Newton's Universal Law of gravitation, which includes identifying problems where it is applicable, identifying the quantities involved in the formula (masses, and distance between them), and using it as part of a Newton's second law problem involving gravitating bodies.
... connect g (little g, 9.8 m/s^2) to G (big G, the constant in Newton's law of University gravity), and extend this connection to other planets where the value of "g" might be different than earth.
... be able to use Kepler's third law to relate period, orbital radius, and the mass of the "central body", both quantitatively and qualitatively.
... Use Newton's law of gravity (with Newton's 2nd law, and the basic definition of speed) to relate orbital speed (in a uniform circular orbit) to radius. (Work out the formula for yourself, it's good practice! Use F=ma, with F= F_grav, and a = a_centrip, and solve for v..)

... know the formula for gravitational potential energy, including proper sign, and the convention that we choose U=0 at infinity.

... Use and interpret "potential energy graphs" for gravity problems

... Know the formula for "escape speed", and use conservation of energy to solve problems involving escape from (or motion from one orbit or height to another) in gravitational problems.

... use conservation of energy in circular orbit problems to related PE, KE, total E, and radius

Momentum Chapter 9
... use the basic definition of momentum (mv) to compute momentum of objects and systems of objects. This includes recognizing the VECTOR nature of momentum, and thus being able to add vectors when you have a system, and find specific components (x, or y) of momentum.
...use the basic definition of impulse (Change in momentum) to be able to compute impulse given initial and final momenta. (That includes 2-dimensional situations where you are subtracting vectors, and 1-d situations where you must consider the SIGNS of the momenta involved, not just their magnitudes)
... relate change in momentum to force and time intervals (F = Delta p / delta t)
... know the principle of conservation of momentum, which means recognizing situations where it applies (generally, systems where there is no EXTERNAL net force) and be able to use it to solve basic problems, typically involving collisions or explosions
... know the terminology "elastic, inelastic, and totally inelastic" collisions, and be able to relate "before and after" quantitaties in all 3 of those cases.
... be able to recognize "ballistic pendulum" problems where a collision happens (involving conservation of momentum, for "immediately before to immediately after" the crash), followed up by something further (like a pendulum rising, or a spring compressing, or a combined system rising in the air) where the second portion involves a different principle, like conservation of energy.

...be able to compute the center of mass of a system of pointlike-masses, and use this to compute v_cm or a_cm.

...Use Newton's law for systems of objects: F_net, external = M_system*a_cm = d(P_system)/dt. The most common application here would be for a system of disconnected objects experiencing zero external (net) force but interacting with one another - in this case, the total momentum of the entire system is constant, and the center of mass does not accelerate. If it starts at rest, it remains at rest.

Rotational Motion Chapter 10

... Define and recognize the standard "rotational kinematics" variables: theta, omega (velocity) and alpha (acceleration).

... relate rotational to linear variables for circular motion ( v = omega*r, a_tan= alpha*r, and a_centrip=omega^2*r).

... Know and be able to apply the simple "constant acceleration" formulas for rotations about a fixed axis.

... Compute torque (including in situations where the force is *not* perpendicular to the line from the axis to the force) ALso compute net torque (knowing and using our sign conventions for + and - theta, omega, alpha, and torque) , andbe able to compute momentum of inertia of compound objects built out of point masses.

... Use Torque_net = I*alpha in problems involving rotational acceleration (and, for spinning wheels, be able to relate alpha with the acceleration of points on the edge)

... Know how to compute rotational kinetic energy for objects spinning about a fixed axis, but also for rolling objects

... relate rotational omega to v_cm for rolling objects, and similarly, relate alpha to a_cm, and distance traveled by a rolling whell to Delta(theta)

... Use conservation of energy for rolling objects.

Rotational vectors and angular momentum Chapter 11

... compute the vector cross product of two vectors

... figure out the direction of torque when r and F vectors are given, and the direction of angular velocity (or angular momentum) given the rotation of an object.

... deduce the direction of angular acceleration given a change in angular velocities.

... compute angular momentum given r and momentum, and/or given "I" and "omega" for rotating objects.

... use the principle of conservation of angular momentum to solve rotational "collision" problems. This includes recognizing WHEN conservation of angular momentum applies (when the system is isolated, so there are no "external" torques. Internal friction is fine, though, it doesn't affect conservation of angular momentum)

Static Equilibrium Chapter 12

... Know and use the conditions for static equilbrium (net force=0, net torque=0)

... Be able to found torque about any axis (in 2D), and realize that for stability you are free to choose your axis.

... qualitatively recognize situations of "stability".

Simple Harmonic Motion ("SHM", or oscillations) Chapter 13

... Recognize when SHM will occur

... Be able to identify the amplitude, frequency, angular frequency, and period of SHM

... Be able to write down the mathematical formula for simple harmonic motion, x(t) = A cos(omega*t+phi), and know what aspects of the motion and the graph "A", "omega", and "phi" tell you (e.g. how they relate to amplitude, frequency, period, and the pictorial graph of motion)

... Know how angular frequency relates to the mass and spring constant of a simple spring.

... Be able to relate x(t), v(t), and a(t) (position, velocity, and acceleration) when you have SHM. (in formulas and pictures)

... Use conservation of energy to determineand relate total energy, KE and PE, and as a result "maximum amplitude" or "max speed". You should be able to interpret our usual "energy plot" (energy as a function of position).

Fluids Chapter 15

... know and use the definitions of density (rho= mass/volume) and pressure (= force/area)

... calculate pressure as you go down to a depth in a fluid (including the addition of atmospheric pressure)

... be able to use Pascal's principle (that pressure is the same at a given depth) to draw basic conclusions about water levels and pressure differences in funny-shaped containers

... Know Archimede's principle: be able to state it, and use it to compute the buoyant force on fully submerged objects

... Understand how Archimede's principle still applies when objects are floating (recognizing that the "fluid displaced" is no longer the full volume of the object)

... be able to use free body diagrams to determine unknown forces in situations involving fully, or partially immersed objects.

Waves Chapter 14

... be able to identify and distinguish longitudinal and transverse waves

... identify wave features and translate between physical pictures, written descriptions, and mathematical formulas, including definitions of all the following terms: Amplitude, frequency, angular frequency, period, wavelength, wave number (k), wave speed, displacement, transverse velocity.

... be able to use the relation lambda * frequency = speed of wave, including knowing what each of those variables depends on (and in particular that the speed of the wave depends on the medium only)

...use sin and cos functions to describe traveling sinusoidal waves, and relate the "parameters" in the formula to the words above (like frequency, amplitude, wave number, etc)

... be able to determine the direction of a traveling wave from the formula for the wave, even if it is not sinusoidal

... use the principle of superposition to graphically (or mathematically) determine the result when two waves "pass through" one another.

... be able to define "standing wave", and use graphical means to relate wavelength and frequency for different "modes" of vibration on a string or tube.

There may be one or two more topics to come for the final (perhaps standing waves), depends how far we get the last 2 weeks of the term, so stay tuned here! But, there will not be any questions on heat or thermodynamics (Ch 16 or beyond).

___________________________________________________________________________________________________

Consider "power posing" before your next exam!